
Se presentan preguntas relacionadas con la función inversa para pares ordenados, funciones lineales, de raíz cúbica, raíz cuadrada, logarítmicas y exponenciales, junto con sus soluciones detalladas. Las respuestas se verifican algebraica y gráficamente utilizando las propiedades de una función dada y su inversa. Para ser más efectivo, se recomienda resolver las preguntas en orden, ya que cada una facilita la comprensión de la siguiente.
Contenido de la Página
a) Encuentra la inversa de la función \( f \) dada por: \[ f = \{( -2 , 0) , (0 , 1) , (2 , 3) , (3 , 4)\} \] b) Encuentra el dominio y rango de la inversa de \( f \).
c) Sea \( f^{-1} \) la inversa de \( f \). Evalúa: \[ f(f^{-1}(1)) \; , \; f^{-1}(f(0)) \; , \; f^{-1}(f(2)) \; , \; f(f^{-1}(3)) \]
d) Grafica \( f \) y \( f^{-1} \) en el mismo sistema de ejes rectangulares y escribe todas las propiedades de \( f \) y su inversa \( f^{-1} \).
a) La inversa de f se encuentra intercambiando la entrada y salida de la función dada. Por lo tanto, la inversa de f está dada por: \[ f^{-1} = \{(0 , -2) , (1 , 0) , (3 , 2) , (4 , 3)\} \]
b) Dominio de \( f^{-1} \): \( \{0 , 1 , 3 , 4\} \)
Rango de \( f^{-1} \): \( \{-2 , 0 , 2 , 3\} \)
c) \[ f(f^{-1}(1)) = f(0) = 1 \] \[ f^{-1}(f(0)) = f^{-1}(1) = 0 \] \[ f^{-1}(f(2)) = f^{-1}(3) = 2 \] \[ f(f^{-1}(3)) = f(4) = 3 \]
d) La gráfica de \( f \) (azul) y \( f^{-1} \) (rojo) se muestran a continuación.

Importante: Observa las siguientes propiedades de \( f \) y su inversa \( f^{-1} \).
1) La gráfica de \( f \) y la gráfica de \( f^{-1} \) son reflejos una de la otra sobre la línea \( y = x \).
2) Las intersecciones x e y en la gráfica de \( f \) se convierten en intersecciones y e x, respectivamente, en la gráfica de \( f^{-1} \).
3) El dominio y rango de \( f \) son el rango y dominio, respectivamente, de \( f^{-1} \).
4) \( f(f^{-1}(x)) = x \) y \( f^{-1}(f(x)) = x \).
5) Si la función \( f \) es la inversa de la función \( g \), entonces la función \( g \) es la inversa de la función \( f \) (una función y su inversa forman un par de funciones).
Encuentra la inversa de la función lineal \( f(x) = 2x + 2 \) y grafica \( f \) y su inversa en el mismo sistema de ejes.
Cómo encontrar la inversa:
Paso 1: Reemplaza \( f(x) \) por \( y \) y reescribe la función como una ecuación: \[ y = 2x + 2 \]
Paso 2: Intercambia \( x \) y \( y \) en la ecuación anterior: \[ x = 2y + 2 \]
Paso 3: Resuelve la ecuación anterior para \( y \): \[ 2y = x - 2 \] \[ y = \frac{1}{2}x - 1 \]
Paso 4: Escribe la inversa usando la notación de función inversa: \[ f^{-1}(x) = \frac{1}{2}x - 1 \]
Paso 5: Verifica la respuesta obtenida usando las propiedades: \( f(f^{-1}(x)) = x \) y \( f^{-1}(f(x)) = x \). \[ f(f^{-1}(x)) = 2(f^{-1}(x)) + 2 = 2\left(\frac{1}{2}x - 1\right) + 2 = x - 2 + 2 = x \] \[ f^{-1}(f(x)) = \frac{1}{2} f(x) - 1 = \frac{1}{2}(2x + 2) - 1 = x + 1 - 1 = x \]
Las gráficas de \( f \) y \( f^{-1} \) se muestran a continuación. Se puede ver fácilmente que las gráficas son reflejos una de la otra sobre la línea \( y = x \). Este es un método gráfico para verificar si un par de funciones son inversas entre sí.
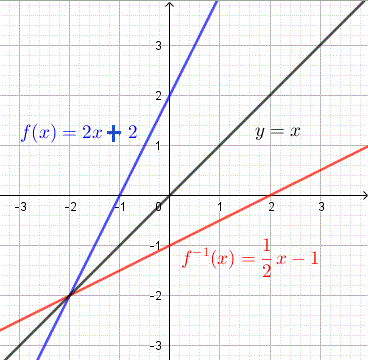
Encuentra la inversa de la función \( g(x) = \sqrt[3]{x - 1} \) y grafica \( g \) y su inversa en el mismo sistema de ejes.
Paso 1: Reescribe la función como una ecuación: \[ y = \sqrt[3]{x - 1} \]
Paso 2: Intercambia x e y: \[ x = \sqrt[3]{y - 1} \]
Paso 3: Resuelve la ecuación anterior para \( y \). Eleva ambos lados de la ecuación a la potencia 3 y simplifica: \[ x^3 = (\sqrt[3]{y - 1})^3 \] \[ x^3 = y - 1 \] \[ y = x^3 + 1 \]
Paso 4: Usa la notación de función inversa para escribir: \[ g^{-1}(x) = x^3 + 1 \]
Paso 5: Verifica algebraicamente la respuesta usando las propiedades: \( g(g^{-1}(x)) = x \) y \( g^{-1}(g(x)) = x \). \[ g(g^{-1}(x)) = \sqrt[3]{g^{-1}(x) - 1} = \sqrt[3]{x^3 + 1 - 1} = \sqrt[3]{x^3} = x \] \[ g^{-1}(g(x)) = (g(x))^3 + 1 = (\sqrt[3]{x - 1})^3 + 1 = x - 1 + 1 = x \]
Podemos verificar fácilmente que las gráficas de las funciones \( g \) y \( g^{-1} \), mostradas a continuación, son reflejos una de la otra sobre la línea \( y = x \) y, por lo tanto, son inversas entre sí.

Encuentra la inversa de la función \( h(x) = \ln(x - 1) \) y grafica \( h \) y su inversa en el mismo sistema de ejes.
Paso 1: Reescribe la función como una ecuación: \[ y = \ln(x - 1) \]
Paso 2: Intercambia x e y: \[ x = \ln(y - 1) \]
Paso 3: Resuelve la ecuación anterior para \( y \) convirtiendo la expresión logarítmica a expresión exponencial: \[ y - 1 = e^x \] \[ y = e^x + 1 \]
Paso 4: Usa la notación de función inversa: \[ h^{-1}(x) = e^x + 1 \]
Paso 5: Verifica algebraicamente la respuesta: \[ h(h^{-1}(x)) = \ln(h^{-1}(x) - 1) = \ln(e^x + 1 - 1) = \ln(e^x) = x \] \[ h^{-1}(h(x)) = e^{h(x)} + 1 = e^{\ln(x - 1)} + 1 = x - 1 + 1 = x \]
Las gráficas de las funciones \( h \) y \( h^{-1} \) se muestran a continuación. Las dos gráficas son reflejos una de la otra sobre la línea \( y = x \) y, por lo tanto, son inversas entre sí.

Encuentra la inversa de la función \( m(x) = \sqrt{x + 2} \)
Paso 1: Reescribe la función dada como una ecuación: \[ y = \sqrt{x + 2} \]
Paso 2: Intercambia x e y: \[ x = \sqrt{y + 2} \]
Paso 3: Resuelve la ecuación anterior para \( y \) elevando ambos lados al cuadrado: \[ x^2 = (\sqrt{y + 2})^2 \] \[ x^2 = y + 2 \] \[ y = x^2 - 2 \]
Nota: \( y = x^2 - 2 \) no es una función uno a uno y, por lo tanto, no es invertible. Necesitamos restringir su dominio. El dominio de una función inversa es el rango de la función dada \( y = \sqrt{x + 2} \), que está dado por el intervalo \( [0, \infty) \).
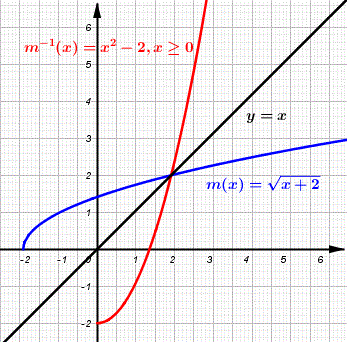
Paso 4: Usa la notación de función inversa: \[ m^{-1}(x) = x^2 - 2 \; , \; x \ge 0 \; \text{(dominio restringido)} \]
Paso 5: Verifica algebraicamente la respuesta: \[ m(m^{-1}(x)) = \sqrt{m^{-1}(x) + 2} = \sqrt{x^2 - 2 + 2} = \sqrt{x^2} = |x| = x \; \text{porque} \; x \ge 0 \] \[ m^{-1}(m(x)) = (m(x))^2 - 2 = (\sqrt{x + 2})^2 - 2 = x + 2 - 2 = x \]
Las gráficas de \( m \) y \( m^{-1} \) mostradas a continuación son reflejos una de la otra sobre la línea \( y = x \) y, por lo tanto, son inversas entre sí.
Encuentra la inversa de la función \( t(x) = \dfrac{1}{x-1} \)
Paso 1: Reescribe la función dada como una ecuación: \[ y = \dfrac{1}{x-1} \]
Paso 2: Intercambia x e y: \[ x = \dfrac{1}{y - 1} \]
Paso 3: Resuelve la ecuación anterior para \( y \) multiplicando ambos lados por \( y - 1 \) y simplificando: \[ x(y - 1) = 1 \] \[ xy - x = 1 \] \[ xy = x + 1 \] \[ y = \dfrac{x + 1}{x} \]
Paso 4: Usa la notación de función inversa para escribir: \[ t^{-1}(x) = \dfrac{x+1}{x} \]
Paso 5: Verifica algebraicamente la respuesta: \[ t(t^{-1}(x)) = \dfrac{1}{t^{-1}(x) - 1} = \dfrac{1}{\frac{x+1}{x} - 1} = \dfrac{1}{\frac{x+1 - x}{x}} = \dfrac{1}{\frac{1}{x}} = x \] \[ t^{-1}(t(x)) = \dfrac{t(x) + 1}{t(x)} = \dfrac{\frac{1}{x-1} + 1}{\frac{1}{x-1}} = \dfrac{\frac{1 + (x-1)}{x-1}}{\frac{1}{x-1}} = \dfrac{\frac{x}{x-1}}{\frac{1}{x-1}} = x \]
Podemos verificar que las gráficas de la función \( t \) y su inversa \( t^{-1} \), mostradas a continuación, son reflejos una de la otra sobre la línea \( y = x \) y, por lo tanto, son inversas entre sí.
