Encuentra el Volumen de una Pirámide Cuadrada Usando Integrales
Encuentra la fórmula para el volumen de una pirámide cuadrada usando integrales en cálculo.
Problema : Se muestra una pirámide en la figura siguiente. Su base es un cuadrado de lado \( a \) y es ortogonal al eje y. La altura de la pirámide es \( H \). Usa integrales y sus propiedades para encontrar el volumen de la pirámide cuadrada en términos de \( a \) y \( H \).
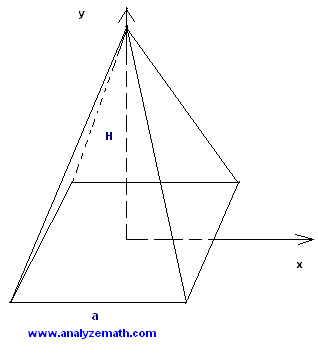
Solución al problema:
Primero posicionemos la pirámide de manera que dos lados opuestos de la base cuadrada sean perpendiculares al eje x y el centro de su base esté en el origen del sistema de ejes x-y. Si miramos la pirámide en una dirección ortogonal al plano x-y, parecerá una forma bidimensional como se muestra a continuación. AC es la altura inclinada.
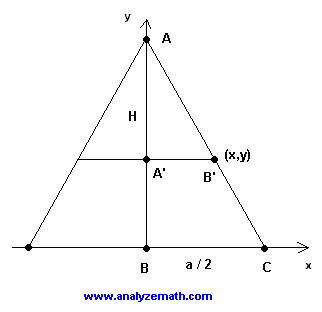
Sea \( x = A'B' \) la longitud de la mitad del lado del cuadrado a una altura \( y \). El área \( A \) del cuadrado a una altura \( y \) está dada por:
\[ A(x) = (2x)^2 \]
El volumen se encuentra sumando todos los volúmenes \( A \, dy \) que forman la pirámide desde \( y = 0 \) hasta \( y = H \). Por lo tanto,
\[ \text{Volumen} = \int_{0}^{H} A^2 \, dy \]
\[ = 4 \int_{0}^{H} x^2 \, dy \]
Ahora usamos el hecho de que los triángulos ABC y AB'C' son similares y, por lo tanto, las longitudes de sus lados correspondientes son proporcionales para escribir:
\[ \frac{a/2}{x} = \frac{H}{H - y} \]
Ahora resolvemos lo anterior para \( x \) para obtener
\[ x = \frac{a (H - y)}{2 H} \]
Ahora sustituimos \( x \) en la integral que da el volumen para obtener
\[ \text{Volumen} = 4 \left(\frac{a}{2H}\right)^2 \int_{0}^{H} (H - y)^2 \, dy \]
Definamos \( t \) como
\[ t = H - y \quad \text{y} \quad dt = - dy \]
Sustituye y cambia los límites de integración para escribir el volumen de la siguiente manera:
\[ \text{Volumen} = 4 \left(\frac{a}{2H}\right)^2 \int_{H}^{0} t^2 (- dt) \]
Evalúa la integral y simplifica
\[ \text{Volumen} = 4 \left(\frac{a}{2H}\right)^2 \left[\frac{H^3}{3}\right] \]
\[ \text{Volumen} = \frac{a^2 H}{3} \]
El volumen de una pirámide cuadrada se da por el área de la base multiplicada por un tercio de la altura de la pirámide.
