Se discuten las gráficas de las funciones seno y coseno de la forma: \[ \Large \mathbf { \color{red}{ y = a \sin(b x + c) + d}} \] y \[ \Large \mathbf { \color{red}{ y = a \cos(b x + c) + d}} \] con varios ejemplos que incluyen soluciones detalladas.
Comenzamos con la gráfica de la función seno básica \( y = \sin(x) \) y la función coseno básica \( g(x) = \cos(x) \), luego presentamos ejemplos de cómo graficar versiones transformadas de estas mismas funciones. Una forma efectiva de usar este tutorial es empezar desde el principio y revisar los ejemplos en orden.
Encuentra el rango y el periodo de la función \( y = \sin(x) \) y grafícala.
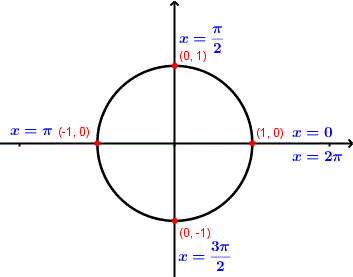
Un círculo unitario (con radio 1) centrado en el origen del sistema de ejes rectangulares tiene 4 puntos especiales correspondientes a 5 ángulos cuadrantales \( (0, \dfrac{\pi}{2}, \pi, \dfrac{3\pi}{2}, 2\pi) \), como se muestra en la figura 1. Las coordenadas \( x \) e \( y \) de un punto en el círculo unitario son el coseno y el seno, respectivamente, del ángulo correspondiente.

Siendo \( x \) el ángulo en posición estándar, del círculo unitario podemos concluir lo siguiente:
El rango de \( \sin(x) \) (las coordenadas \( y \)) es el conjunto de todos los valores en el intervalo: \[ [-1, 1] \quad \text{o en forma de desigualdad:} \quad -1 \leq \sin(x) \leq 1 \]
Un ciclo de \( \sin(x) \) puede comenzar en \( x = 0 \) y terminar en \( x = 2\pi \), después de lo cual los valores de \( \sin(x) \) se repiten, como se muestra en el círculo unitario. Por lo tanto, decimos que \( \sin(x) \) tiene un periodo igual a \( 2\pi \).
Necesitamos valores de \( \sin(x) \) para diferentes valores de \( x \) para graficarla. Usaremos la coordenada \( y \) (que da \( \sin(x) \)) de los mismos 5 ángulos cuadrantales correspondientes a la variable \( x (0, \dfrac{\pi}{2}, \pi, \dfrac{3\pi}{2}, 2\pi) \), de los cuales 3 valores \( (0, \pi, 2\pi) \) son ceros de \( \sin(x) \), un valor \( (\dfrac{\pi}{2}) \) da un valor máximo a \( \sin(x) \) y un valor \( ( \dfrac{3\pi}{2} ) \) da un valor mínimo a \( \sin(x) \), como se muestra en la siguiente tabla.
\[ \begin{array}{|c|c|c|} \hline x & y = \sin(x) \\ \hline 0 & 0 \\ \dfrac{\pi}{2} & 1\\ \pi & 0 \\ 3\dfrac{\pi}{2} & -1 \\ 2 \pi & 0 \\ \hline \end{array} \]La gráfica de \( y = \sin(x) \) se muestra a continuación en un periodo desde \( 0 \) hasta \( 2\pi \) (línea sólida) y otros periodos (línea punteada).
.gif)
Encuentra el rango y el periodo de la función \( y = \cos(x) \) y grafícala.
Usaremos los mismos 4 puntos especiales correspondientes a 5 ángulos cuadrantales \( 0, \dfrac{\pi}{2}, \pi, \dfrac{3\pi}{2} \text{ y } 2\pi \), como se muestra en el círculo unitario (figura 1 anterior). \( \cos(x) \) está dada por la coordenada \( x \) de un punto en el círculo unitario correspondiente al ángulo \( x \) en posición estándar.
Del círculo unitario podemos concluir lo siguiente:
El rango de \( \cos(x) \) es el conjunto de todos los valores en el intervalo \([-1, 1]\); en forma de desigualdad: \[ -1 \leq \cos(x) \leq 1 \]
Un ciclo de \( \cos(x) \) puede comenzar en \( x = 0 \) y terminar en \( x = 2\pi \), después de lo cual el valor de \( \cos(x) \) se repite periódicamente. Por lo tanto, concluimos que \( \cos(x) \) tiene un periodo igual a \( 2\pi \).
Usamos los valores de \( \cos(x) \) para diferentes valores de \( x \) del círculo unitario (ver figura 1). Usaremos la coordenada \( x \) (que da \( \cos(x) \)) de los mismos 5 ángulos cuadrantales correspondientes a la variable \( x \): \( 0, \dfrac{\pi}{2}, \pi, \dfrac{3\pi}{2}, \text{ y } 2\pi \). De estos, dos valores (\( 0, 2\pi \)) dan el valor máximo \( 1 \) de \( \cos(x) \), dos valores \( \dfrac{\pi}{2} \) y \( \dfrac{3\pi}{2} \) dan ceros de \( \cos(x) \), y un valor \( \pi \) da un valor mínimo a \( \cos(x) \), como se muestra en la siguiente tabla.
\[ \begin{array}{|c|c|c|} \hline x & y = \cos(x) \\ \hline 0 & 1 \\ \dfrac{\pi}{2} & 0 \\ \pi & -1 \\ 3\dfrac{\pi}{2} & 0 \\ 2 \pi & 1 \\ \hline \end{array} \]La gráfica de \( \cos(x) \) se muestra a continuación en un periodo desde \( 0 \) hasta \( 2\pi \) (línea sólida) y más periodos (línea punteada).
.gif)
Encuentra el rango y el periodo de la función \( y = 3\sin(x) \) y grafícala.
Comparando la función dada \( y = 3 \sin(x) \) y la función seno básica \( y = \sin(x) \), hay un factor de multiplicación de 3. No hay estiramiento horizontal ni desplazamiento, ya que la variable \( x \) aparece de la misma "manera" en ambas funciones. \[ \text{Periodo} = 2\pi \]
Ya hicimos una tabla para \( \sin(x) \) arriba; extendámosla e incluyamos la función dada \( y = 3 \sin(x) \) para graficar.
Nota: Para obtener valores para la función \( 3 \sin(x) \), multiplicas los valores de la función \( \sin(x) \) por 3, como se muestra en la siguiente tabla.
De la tabla: \[ \text{Rango: } -3 \leq 3 \sin(x) \leq 3 \]
\[ \begin{array}{|c|c|c|} \hline x & \sin(x) & y = 3 \sin(x) \\ \hline 0 & 0 & 0 \\ \dfrac{\pi}{2} & 1 & 3 \\ \pi & 0 & 0 \\ 3\dfrac{\pi}{2} & -1 & -3 \\ 2 \pi & 0 & 0 \\ \hline \end{array} \]La gráfica de \( 3 \sin(x) \) se muestra a continuación en un periodo desde 0 hasta \( 2\pi \) y, como se esperaba, hay un estiramiento vertical de un factor de 3 (comparado con \( y = \sin(x) \), en rojo). El periodo no cambió, pero el rango ahora es: \( [-3, 3] \) o en forma de desigualdad: \( -3 \leq 3 \sin(x) \leq 3 \).
.gif)
Encuentra el rango y el periodo de la función \( y = -2 \cos(x) \) y grafícala.
Comparando la función dada \( y = - 2 \cos(x) \) y la función coseno básica \( y = \cos(x) \), hay un estiramiento vertical de un factor de 2 y también una reflexión en el eje \( x \) debido al signo menos en -2. No hay estiramiento horizontal ni desplazamiento, ya que la variable \( x \) aparece de la misma "manera" en ambas funciones.
Periodo = \( 2\pi \)
Ya se hizo una tabla para \( \cos(x) \) arriba; extendámosla para incluir la función dada \( y = - 2 \cos(x) \) para graficar.
De la tabla; rango: \( -2 \leq -2 \cos(x) \leq 2 \)
En general, el rango de funciones de la forma \( y = a \sin(x) \) o \( y = a \cos(x) \) está dado por el intervalo \[ [ - |a| , |a| ] \quad \text{o en forma de desigualdad:} \quad - |a| \le y \le |a| \]
\[ \begin{array}{|c|c|c|} \hline x & \cos(x) & y = -2 \cos(x) \\ \hline 0 & 1 & -2 \\ \dfrac{\pi}{2} & 0 & 0 \\ \pi & -1 & 2 \\ 3\dfrac{\pi}{2} & 0 & 0 \\ 2 \pi & 1 & -2 \\ \hline \end{array} \]La gráfica de \( -2 \cos(x) \) se muestra a continuación en un periodo desde \( 0 \) hasta \( 2\pi \) (línea sólida azul) comparada con \( y = \cos(x) \) (rojo) y podemos ver que hay un estiramiento de factor 2 y una reflexión.
.gif)
Encuentra el periodo de la función \( y =\sin(2 x) \) y grafícala.
Comparando la función dada \( y = \sin(2 x) \) y la función seno básica \( y = \sin(x) \), hay una compresión horizontal de un factor de \( 2 \) debido al \( 2x \) en \( \sin(2 x) \).
Explicación:
Para que la función \( y =\sin(2 x) \) complete un periodo, \( 2 x \) tendrá que ser como sigue: \[ 0 \leq 2x \leq 2\pi \]
Divide por \( 2 \) todos los términos de la desigualdad anterior para obtener: \[ 0 \leq x \leq \pi \] Este es el intervalo de un periodo que se usará para graficar \( y =\sin(2 x) \).
Por lo tanto, el periodo de \( \sin(2x) \) está dado por: \[ \pi - 0 = \pi \]
En general, el periodo de funciones de la forma \( y = \sin( b x) \) o \( y = \cos( b x) \) está dado por \[ \dfrac{2\pi}{|b|} \] (el periodo siempre es positivo).
Una tabla para \( \sin(2 x) \) se hace de manera similar a \( y = \sin(x) \), con una diferencia en los valores de \( x \) sobre un periodo desde \( 0 \) hasta \( \pi \) (un periodo).
Los valores \( x = 0, \pi/4, \pi/2, 3\pi/4, \pi \) dividen el periodo en 4 intervalos iguales.
\[ \begin{array}{|c|c|c|} \hline x & y = \sin(2 x) \\ \hline 0 & 0 \\ \dfrac{\pi}{4} & 1 \\ \dfrac{\pi}{2} & 0 \\ 3\dfrac{\pi}{4} & -1 \\ \pi & 0 \\ \hline \end{array} \]La gráfica de \( y = \sin(2 x) \) se muestra a continuación en un periodo desde \( 0 \) hasta \( \pi \) (línea sólida azul) comparada con \( y =\sin(x) \) que tiene un periodo de \( 2\pi \) (rojo).
.gif)
Encuentra el periodo y el desfase (cambio de fase) de la función \( y = \cos\left(2x - \dfrac{\pi}{4}\right) \) y grafícala.
Reescribe la función dada como: \[ y = \cos\left(2(x - \dfrac{\pi}{8})\right) \]
Primero ignoramos el término \( -\dfrac{\pi}{8} \) y definimos un periodo para \( y = \cos(2x) \): \[ 0 \leq 2x \leq 2\pi \] Divide todos los términos por 2: \[ 0 \leq x \leq \pi \] El periodo es \( \pi \), como ya se calculó arriba.
Para que la función \( y = \cos\left(2(x - \dfrac{\pi}{8})\right) \) complete un periodo, la expresión \( 2(x - \dfrac{\pi}{8}) \) tendrá que ser: \[ 0 \leq 2(x - \dfrac{\pi}{8}) \leq 2\pi \] Divide todos los términos por 2: \[ 0 \leq x - \dfrac{\pi}{8} \leq \pi \] Suma \( \dfrac{\pi}{8} \) a todos los términos: \[ \dfrac{\pi}{8} \leq x \leq \pi + \dfrac{\pi}{8} \] Este es el intervalo de un periodo que se usará para graficar \( y = \cos\left(2x - \dfrac{\pi}{4}\right) \).
Cuando comparamos el intervalo de un periodo para \( \cos(2x) \), que es \[ 0 \leq x \leq \pi \] y el intervalo para un periodo de \( \cos\left(2(x - \dfrac{\pi}{8})\right) \), que es \[ \dfrac{\pi}{8} \leq x \leq \pi + \dfrac{\pi}{8} \] la única diferencia es el desfase hacia la derecha por \( \dfrac{\pi}{8} \).
En general, el desfase de funciones de la forma \( y = \sin(bx + c) \) o \( y = \cos(bx + c) \) está dado por \[ -\dfrac{c}{b} \] Si el desfase es positivo, el desplazamiento es hacia la derecha; si es negativo, hacia la izquierda.
Construimos la tabla de valores de la siguiente manera:
Hemos visto arriba que en este ejemplo un periodo comienza en \( x = \dfrac{\pi}{8} \) y termina en \( x = \pi + \dfrac{\pi}{8} = \dfrac{9\pi}{8} \). Por lo tanto, comenzamos la tabla usando estos dos puntos.

Luego encontramos el valor medio entre \( x = \pi/8 \) y \( x = 9\pi/8 \), calculado como: \[ \dfrac{1}{2} \left( \dfrac{\pi}{8} + \dfrac{9\pi}{8} \right) = \dfrac{5\pi}{8} \] y lo ponemos en la tabla.

Luego encontramos el valor medio entre \( x = \pi/8 \) y \( 5\pi/8 \), calculado como: \[ \dfrac{1}{2} \left( \dfrac{\pi}{8} + \dfrac{5\pi}{8} \right) = \dfrac{3\pi}{8} \] y el valor medio entre \( 5\pi/8 \) y \( 9\pi/8 \), calculado como: \[ \dfrac{1}{2} \left( \dfrac{5\pi}{8} + \dfrac{9\pi}{8} \right) = \dfrac{7\pi}{8} \] y ponemos todos estos en la tabla como sigue:

Hemos dividido el intervalo de un periodo en 4 intervalos iguales, lo que facilita evaluar la función dada \( y = \cos(2x - \pi/4) \). Completamos la tabla poniendo los valores de la función.

La gráfica de \( y = \cos(2 x - \dfrac{\pi}{4}) \) (azul) se compara con la gráfica de \( \cos(2 x) \) (rojo). Son similares excepto por el desplazamiento de \( \dfrac{\pi}{8} \) hacia la derecha.
.gif)
Encuentra el periodo y el desfase de la función \( y =\sin(3 x + \dfrac{\pi}{3}) \) y grafícala.
El periodo está dado por: \[ \dfrac{2\pi}{|b|} = \dfrac{2\pi}{3} \]
El desfase se calcula como: \[ \dfrac{-c}{b} = \dfrac{-\pi/3}{3} = \dfrac{-\pi}{9} \]
Esperamos que la gráfica de \( y = \sin(3x + \dfrac{\pi}{3}) \) sea la gráfica de \( y = \sin(3x) \) desplazada por \( \dfrac{\pi}{9} \) hacia la izquierda debido al signo menos en el desfase.
Para que la función \( y = \sin(3x + \dfrac{\pi}{3}) \) complete un periodo, la expresión \( 3x + \dfrac{\pi}{3} \) tendrá que ser: \[ 0 \leq 3x + \dfrac{\pi}{3} \leq 2\pi \]
Resuelve la desigualdad anterior para \( x \) para obtener el intervalo correspondiente a un periodo: \[ -\dfrac{\pi}{9} \leq x \leq \dfrac{5\pi}{9} \]
Encuentra los valores medios como se hizo en el ejemplo 6 y completa la tabla de valores.

La gráfica de la función dada \( y =\sin(3 x + \dfrac{\pi}{3}) \) (azul) se compara con la gráfica de \( \sin(3 x) \) (rojo). Son similares excepto por el desplazamiento de \( \dfrac{\pi}{9} \) hacia la izquierda.
.gif)
Encuentra el rango, el periodo y el desfase de la función \( y = - 2\sin(2 x - \dfrac{\pi}{5}) + 1 \) y grafícala.
Sabemos que el rango de \( \sin(2x - \pi/5) \) está dado por el intervalo \([-1, 1]\) o, como desigualdad: \[ -1 \leq \sin(2x - \pi/5) \leq 1 \]
Multiplica todos los términos de la desigualdad por \(-2\) y cambia los símbolos de desigualdad: \[ 2 \geq -2\sin(2x - \pi/5) \geq -2 \]
Suma \(+1\) a todos los términos de la desigualdad y reescribe como: \[ -2 + 1 \leq -2\sin(2x - \pi/5) + 1 \leq 2 + 1 \]
Lo que da el rango de la función dada como: \[ -1 \leq -2\sin(2x - \pi/5) + 1 \leq 3 \]
En general, el rango de la función \( y = a\sin(bx + c) + d \) o \( y = a\cos(bx + c) + d \) está dado por el intervalo \[ [ -|a| + d , |a| + d ] \quad \text{o en forma de desigualdad:} \quad -|a| + d \leq y \leq |a| + d \]
El periodo está dado por: \[ \dfrac{2\pi}{|b|} = \dfrac{2\pi}{|2|} = \pi \]
El desfase está dado por: \[ -\dfrac{c}{b} = -\dfrac{-\pi/5}{2} = \dfrac{\pi}{10} \]
Para graficar \( y = -2\sin(2x - \pi/5) + 1 \) en un periodo, la expresión \( 2x - \pi/5 \) debe pasar por un periodo como sigue: \[ 0 \leq 2x - \pi/5 \leq 2\pi \]
Resuelve la desigualdad anterior para obtener: \[ \dfrac{\pi}{10} \leq x \leq \dfrac{11\pi}{10} \]
Usa el valor más bajo \( \dfrac{\pi}{10} \) y el más alto \( \dfrac{11\pi}{10} \) en la desigualdad anterior (que da un periodo) para construir una tabla de valores dividiendo el periodo en 4 intervalos iguales, como sigue:

Es importante notar que la gráfica en un periodo está inscrita dentro de un rectángulo de longitud desde \( \dfrac{\pi}{10} \) hasta \( \dfrac{11\pi}{10} \) (el intervalo de un periodo encontrado arriba) y un ancho desde el mínimo hasta el máximo (rango) de \( y = - 2\sin(2 x - \dfrac{\pi}{5}) + 1 \), igual a \( -1 \) y \( 3 \), que es el rango ya encontrado.
+1.gif)
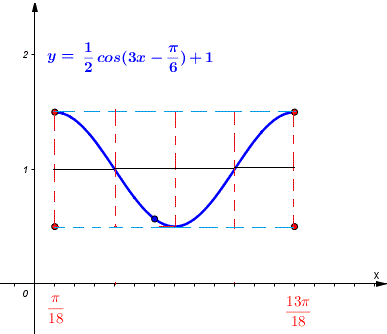
Para la función dada a continuación, encuentra los valores inicial y final de \( x \) en un periodo, el rango y grafícala en un periodo. \[ y = \dfrac{1}{2} \cos\left(3x - \dfrac{\pi}{6}\right) + 1 \]
Un periodo: \( \dfrac{\pi}{18} \leq x \leq \dfrac{13\pi}{18} \), rango: \( [1/2, 3/2] \). Ver gráfica a continuación.