Trigonometry Placement Test Practice with Solutions
The following trigonometry multiple choice questions guide you in assessing your skills and abilities in the following topics: angles in radians and degrees, coterminal angles, trigonometric ratios,
trigonometric identities and formulas, angles in standard position, zeros, maximum, minimum, period, amplitude and graphs of trigonometric functions, polar coordinates, sine and cosine laws, length and area of sectors,
trigonometric equations, angular speed are presented along with their answers and detailed solutions.
Questions for Trigonometry Placement Practice
-
The radian measure of \( \theta = - 220^{\circ} \) is
A) \( -220 \pi \)
B) \( - \dfrac{220}{ \pi} \)
C) \( \dfrac{11}{9} \pi \)
D) \( - \dfrac{11}{9} \pi \)
E) \( \dfrac{11}{9} \)
-
The degree measure of \( \theta = - \dfrac{11 \pi}{4} \) is
A) \( -1980^{\circ} \)
B) \( - 495^{\circ} \)
C) \( 1980^{\circ} \)
D) \( -45^{\circ} \)
E) \( 45^{\circ} \)
-
Which of the following angles is coterminal with the angle \( \theta = - \dfrac{11 \pi}{5} \)
A) \(- \dfrac{4 \pi }{5} \)
B) \( \dfrac{9 \pi }{5} \)
C) \( -\dfrac{6 \pi }{5} \)
D) \( \dfrac{\pi}{5} \)
E) \( \dfrac{9 \pi }{5} \)
-
If \( \theta\) is an acute angle such that \( \cos \theta = 1/4 \), then the exact value of \( \tan \theta \) is equal to
A) \( \sqrt {17} \)
B) \( \dfrac{1}{\sqrt {17}} \)
C) \( 4 \)
D) \( \dfrac{1}{\sqrt {15}} \)
E) \( \sqrt {15} \)
-
What is \( \sin \alpha \) in the figure below?

A) \( \dfrac{3}{5} \)
B) \( \dfrac{4}{5} \)
C) \( \dfrac{4 a}{5} \)
D) \( \dfrac{3 a}{5} \)
E) \( \dfrac{4}{5 a} \)
-
Write the height \( h \) in terms of \( \alpha \), \( \beta \) and the distance \( \bar {CD} = x \).

A) \( \quad h = \dfrac{x}{ \cot \beta - \cot \alpha} \)
B) \( \quad h = \dfrac{x}{ \cot ( \beta + \alpha) } \)
C) \( \quad h = \dfrac{x}{ \tan \beta - \tan \alpha} \)
D) \( \quad h = \dfrac{x}{ \cot \beta} \)
E) \( \quad h = \dfrac{x}{ \cot \alpha - \cot \beta} \)
-
Find the exact value of \( \tan 75^{\circ} \).
A) \( \frac{\sqrt{3}+3}{3} \)
B) \( \dfrac{\sqrt{3}}{3}+1 \)
C) \( \dfrac{3-\sqrt{3}}{3} \)
D) \( 2+\sqrt{3}\)
E) \( \dfrac{1}{2+\sqrt{3}}\)
-
Find the value of \( y \) such that \( \sin \alpha = \dfrac{1}{5} \) and \( \alpha \) is an angle
in standard position whose terminal side passes through the point \( (-2 , y) \).
A) \( 2/5 \)
B) \( - 5/2 \)
C) \( 5/2 \)
D) \( - 1/2 \)
E) \( - 2/5 \)
-
Find the exact value of \( \cot \alpha \) if \( \sin \alpha = - 11/16 \) and \( \sec \alpha \gt 0 \).
A) \( \dfrac{3\sqrt{15}}{11} \)
B) \( -\dfrac{3\sqrt{15}}{11} \)
C) \( -\dfrac{11\sqrt{15}}{45} \)
D) \( \dfrac{11\sqrt{15}}{45} \)
E) \( -\dfrac{1}{2} \)
-
Angle \( \beta \) is in standard position and its terminal side passes through the point \( (2,k) \), where \( k \) is a nonzero real number. Which of the following is true for all possible values of \( k \) ?
A) \( \tan \beta \lt 0 \)
B) \( \sin \beta \gt 0 \)
C) \( \cos \beta = \sqrt{1-sin^2\beta} \)
D) \( \sec \beta \lt 0 \)
E) \( \sin \beta + \cos \beta = 1 \)
-
If \( cos \theta = 1/5 \), find the exact value of \( \cos (\theta + 3\pi) \).
A) \( - 1/5 \)
B) \( 1/5 \)
C) \( - \dfrac{2\sqrt{6}}{5} \)
D) \( 1 \)
E) \( \dfrac{2\sqrt{6}}{5} \)
-
What is the range of the function \( f(x) = - \dfrac{1}{3} \sin(2x-\pi/4) - 3 \)
A) \( \left[ -\dfrac{1}{3} , \dfrac{1}{3} \right] \)
B) \( \left[ -3 , - 3 \right] \)
C) \( \left[ -\dfrac{10}{3} , - \dfrac{8}{3} \right] \)
D) \( \left[ -1 , 1 \right] \)
E) \( \left[ -3 , 0 \right] \)
-
Find all the zeros of the function \( f(x) = 2 \cos (2x - \pi/3) + 1 \) in the interval \( [0,\pi) \).
A) \( \left\{ \dfrac{2\pi}{3} , \dfrac{4\pi}{3} \right\} \)
B) \( \left\{ \dfrac{\pi}{2} \right\} \)
C) \( \left\{ \dfrac{4\pi}{3} \right\} \)
D) \( \left\{ \dfrac{5\pi}{6} \right\} \)
E) \( \left\{ \dfrac{\pi}{2} , \dfrac{5\pi}{6} \right\} \)
-
Find all the values of \( x \) in the interval \( [0,2\pi) \) for which the function \( f(x) = - \sin (x + \pi/6) + 1 \) has a maximum.
A) \( \dfrac{3\pi}{2} \)
B) \( \dfrac{\pi}{2} \)
C) \( \dfrac{5\pi}{3} \)
D) \( \dfrac{4\pi}{3} \)
E) \( \dfrac{2\pi}{3} \)
-
What is the period of the function \( f(x) = - \cos (-\dfrac{x}{4} - 2 \pi) + 10 \)?
A) \( 8\pi \)
B) \( 4\pi \)
C) \( 2\pi \)
D) \( \dfrac{\pi}{4} \)
E) \( - 8\pi \)
-
What is the amplitude of the function \( f(x) = - 2 \cos (-5x - \pi) + 5 \)?
A) \( 7 \)
B) \( 2 \)
C) \( 3 \)
D) \( 1 \)
E) \( - 2 \)
-
Find the equation of a sine function of the form \( f(x) = A \sin(B x + C) + D \), with \( A \gt 0\) and \( B \gt 0\). The graph of function \( f \) has a period equal to \( \pi/2 \), an amplitude equal to \( 2 \) a maximum value equal to \( 3 \) and its smallest positive maximum occurs at \( x = \pi/4 \).
A) \( f(x) = 2 \sin((\pi/2) x - \pi/2 ) \)
B) \( f(x) = 2 \sin(4 x + \pi/2 ) + 1 \)
C) \( f(x) = - 2 \sin(4 x + \pi/2 ) + 3 \)
D) \( f(x) = 2 \sin(4 x - \pi/2 ) + 1 \)
E) \( f(x) = 2 \sin(4 x + \pi/2 ) + 3 \)
-
Find the equation of a function of the form \( f(x) = A \cos(B x + C) \) corresponding the graph below?
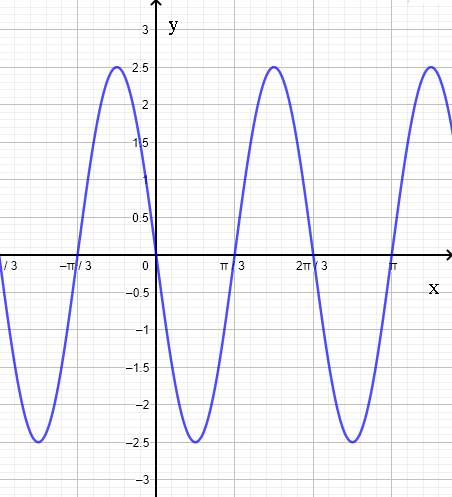
A) \( f(x) = 2.5 \cos(3 x) \)
B) \( f(x) = 2.5 \cos( x + \pi/2) \)
C) \( f(x) = 2.5 \cos(3 x + \pi/2) \)
D) \( f(x) = 2.5 \cos(3 \pi x + \pi/2) \)
E) \( f(x) = 2.5 \cos(3 x + \pi) \)
-
For all values of \( x \) in its domain, the expression \( \dfrac{\cos x - \sin x}{1 - \tan x} \) is equal to
A) \( \dfrac{\cos x - \sin x}{1 + \tan x} \)
B) \( \dfrac{\cos x + \sin x}{1 - \tan x} \)
C) \( \cos x + \sin x \)
D) \( \cos x - \sin x \)
E) \( \dfrac{\cos x + \sin x}{1 + \tan x} \)
-
If \( \alpha \) is an angle in standard position in quadrant II and \( \beta \) is an angle in standard position in quadrant III such that \( \sin \alpha = 9/15 \) and \( \tan \beta = 28/45 \), find the exact value of \( \cos (\alpha - \beta) \).
A) \( \dfrac{265}{276} \)
B) \(-\dfrac{84}{265} \)
C) \(\dfrac{84}{265} \)
D) \(\dfrac{36}{53} \)
E) \(\dfrac{85}{267} \)
-
The lengths of Side \( a \) and \( b \) of a triangle are equal to \( 22 \) centimeters and \( 12 \) centimeters respectively. Find angle \( C \) of the triangle if angle \( A = 42^{\circ} \) (Round your answer to 2 decimal places).
A) \( \approx 116.59^{\circ \:} \)
B) \( \approx 128.90^{\circ \:} \)
C) \( \approx 110.67^{\circ \:} \)
D) \( \approx 98.59^{\circ \:} \)
E) \( \approx 130.78^{\circ \:} \)
-
A triangle has sides \( a \) , \( b \) and \( c \) of lengths \( 24 \), \( 30 \) and \( 32 \) meters respectively. Find the measure of angle \( A \). (Round your answer to 2 decimal places)
A) \( \approx 90.82^{\circ \:}\)
B) \( \approx 45.41^{\circ \:}\)
C) \( \approx 22.71^{\circ \:}\)
D) \( \approx 55.56^{\circ \:}\)
E) \( \approx 65.78^{\circ \:}\)
-
Find all solutions of the equation \( \quad 2 \sin (3 x - \pi/2) + 2 = 1\).
A) \( \quad x_1 = \dfrac{5\pi}{9} + \dfrac{2 n \pi}{3}\)
B) \( \quad x_2 = \dfrac{7\pi}{9} + \dfrac{2 n \pi}{3}\)
C) \( \quad x_1 = \dfrac{7\pi}{6} + 2 n \pi \) , \( \quad x_2 = \dfrac{11\pi}{6} + 2 n \pi \)
D) \( \quad x_1 = \dfrac{7\pi}{6} + \dfrac{2 n \pi}{3}\) , \( \quad x_2 = \dfrac{11\pi}{6} + \dfrac{2 n \pi}{3}\)
E) \( \quad x_1 = \dfrac{5\pi}{9} + \dfrac{2 n \pi}{3}\) , \( \quad x_2 = \dfrac{7\pi}{9} + \dfrac{2 n \pi}{3}\)
-
Find the solution set, in the interval \( [0, 2\pi) \), of the equation \( \quad \tan x + \cot x = - 2\).
A) \( \left\{\dfrac{3 \pi}{4} \right\} \)
B) \( \left\{ \dfrac{7 \pi}{4} \right\} \)
C) \( \left\{\dfrac{\pi}{4} \right\} \)
D) \( \left\{\dfrac{3 \pi}{4} , \dfrac{7 \pi}{4} \right\} \)
E) \( \left\{\dfrac{5 \pi}{4} , \dfrac{7 \pi}{4} \right\} \)
-
Find the solution set, in the interval \( [0,2\pi) \), of the equation \( \quad 2 \sin^2 x + 3\cos^2 x = 5/2 \).
A) \( \left \{ \dfrac{\pi}{4} \right \} \)
B) \( \left \{ \dfrac{\pi}{4} , \dfrac{3 \pi}{4} \right \} \)
C) \( \left \{ \dfrac{3 \pi}{4} \right \} \)
D) \( \left \{\dfrac{7 \pi}{4} \right \} \)
E) \( \left \{ \dfrac{5\pi}{4} , \dfrac{7 \pi}{4} \right \} \)
-
Find the polar coordinates
\( r,\theta \) of the point with rectangular coordinates \( (-2,5) \).
A) \( \left( \sqrt {29} \; , \; \pi + \arctan (5/2) \right) \)
B) \( \left( \sqrt {7} \; , \; \pi - \arctan (5/2) \right) \)
C) \( \left( \sqrt {29} \; , \; \arctan (2/5) \right) \)
D) \( \left( \sqrt {29} \; , \; \pi - \arctan (5/2) \right) \)
E) \( \left( \sqrt {29} \; , \; \arctan (5/2) \right) \)
-
What is the angular speed of an object rotating along a circular path of radius \( 2.1 \) meters at the linear speed of \( 250.4 \) meters per minutes?
A) \( 4.18 \) radians/second
B) \( 1.99 \) radians/second
C) \( 18.97733 \) radians/second
D) \( 21.99 \) radians/second
E) \( 8.97733 \) radians/second
-
Find the area of a sector with a central angle of \( 32^{\circ} \) and an arc length of \( 1.2 \) meters.
A) \( 1.29 \) square meters
B) \( 0.0225 \) square meters
C) \( 12.9 \) square meters
D) \( 38.4 \) square meters
E) \( 129 \) square meters
-
What is the exact value of the expression \( \quad \sin\left(\arccos\left(-0.5\right)+\dfrac{\pi }{4}\right) \)?
A) \( \dfrac{\sqrt 6 + \sqrt 2}{4} \)
B) \( \dfrac{\sqrt 6 - \sqrt 2}{8} \)
C) \( \dfrac{\sqrt 6 - \sqrt 2}{4} \)
D) \( \dfrac{\sqrt 6}{4} \)
E) \( \dfrac{ - \sqrt 2}{4} \)
Answers and Solutions to the Above Questions
- Answer: D
Solution
\( 180^{\circ} \) corresponds to \( \pi \)
Hence: \( -220^{\circ} \) corresponds to: \( \quad -220 \dfrac{\pi}{180} = - \dfrac{11\pi}{9} \)
- Answer: B
Solution
\( \pi \) corresponds to \( 180^{\circ} \)
Hence: \( - \dfrac{11 \pi}{4} \) corresponds to: \( \quad - \dfrac{11 \pi}{4} \dfrac{180}{\pi} = -495^{\circ} \)
- Answer: E
Solution
There is an infinite number of coterminal angles \( \theta_c \) to the given angle \( \quad - \dfrac{11 \pi}{5} \) and they are given by \( \quad \theta_c = - \dfrac{11 \pi}{5} + k (2\pi) \) where \( k \) is an integer.
For \( k = - 1 \), \( \quad \theta_c = - \dfrac{11 \pi}{5} + (-1) (2\pi)= - \dfrac{21\pi}{5} \)
For \( k = 1 \), \( \quad \theta_c = - \dfrac{11 \pi}{5} + (1) (2\pi) = -\dfrac{\pi}{5} \)
For \( k = 2 \), \( \quad \theta_c = - \dfrac{11 \pi}{5} + (2) (2\pi) = \dfrac{9\pi}{5} \)
Hence \( \quad \dfrac{9\pi}{5} \) is a coterminal with the given angle \( - \dfrac{11 \pi}{5} \)
- Answer: E
Solution
Consider angle \( \theta \) in a right triangle as shown below such that \( \quad \cos \theta = \dfrac{1}{4} = \dfrac{b}{c}\)
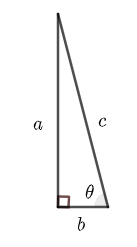
Let \( b = 1\) and \( c = 4\) and use the Pythagorean theorem to find side \( a \): \( \quad a = \sqrt{4^2 - 1^2} = \sqrt {15} \)
Hence \( \quad \tan \theta = \dfrac{a}{b} = \sqrt {15} \)
- Answer: B
Solution
We first use the Pythagorean theorem to find the hypotenuse \( h \) of the triangle: \( \quad h = \sqrt{(4a)^2+(3a)^2} = \sqrt{25 a^2} = 5 a \)
\( \quad \sin \alpha = \dfrac{4 a}{5 a} = \dfrac{4}{5} \)
- Answer: A
Solution
Use the two right triangles to express \( \quad \cot \alpha \) and \( \cot \beta \) as: \( \quad \cot \alpha = \dfrac{\bar{BC}}{h} \) and \( \quad \cot \beta = \dfrac{\bar{BC}+x}{h} \)
Rewrite the above equations as: \( \quad \bar{BC} = h \cot \alpha \) and \( \bar{BC} + x = h \cot \beta \)
Subtract the first equation from the second to obtain: \( \quad \bar{BC} + x - \bar{BC} = h \cot \beta - h \cot \alpha \)
Simplify and solve the above for \( h \) to obtain: \( \quad h = \dfrac{x}{ \cot \beta - \cot \alpha} \)
- Answer: D
Solution
Express \( 75^{\circ} \) as a sum of two special angles. \( 75^{\circ} = 30^{\circ} + 45^{\circ} \)
Hence \( \tan 75^{\circ} = \tan (30^{\circ} + 45^{\circ}) = \dfrac{\tan 30^{\circ}+\tan 45^{\circ}}{1 - \tan 30^{\circ}\tan 45^{\circ}} \)
Knowing that \( \tan 30^{\circ} = \dfrac{\sqrt{3}}{3} \) and \( \tan 45^{\circ} = 1 \), evaluate: \( \tan 75^{\circ} = \dfrac{\dfrac{\sqrt{3}}{3}+1}{1-\dfrac{\sqrt{3}}{3}} = 2+\sqrt{3}\)
- Answer: E
Solution
\( \alpha \) is an angle in standard position and therefore: \( \quad \sin \alpha = \dfrac{y}{-2} = \dfrac{1}{5} \)
Solve the above equation for \( y \) to obtain: \( \quad y = - 2/5 \)
- Answer: B
Solution
Since \( \sec \alpha \gt 0 \), \( \cos \alpha = \dfrac{1}{\sec \alpha} \gt 0 \)
\( \cos \alpha = \sqrt {1-\sin^2 \alpha} = \dfrac{3\sqrt{15}}{16} \)
Hence: \( \cot \alpha = \dfrac{ \cos \alpha}{ \sin \alpha} = \dfrac{ \dfrac{3\sqrt{15}}{16}}{ - 11/16} = -\dfrac{3\sqrt{15}}{11}\)
- Answer: C
Solution
The \( x \) coordinate of the given point \( (2,k) \) is positive and therefore \( \quad \cos \beta = \dfrac{2}{\sqrt{2^2+k^2}} \) is always positive.
The signs of \( \tan \beta = \dfrac{k}{2} \) and \( \sin \beta = \dfrac{k}{\sqrt{2^2+k^2}} \) depends on \( k \), hence A) and B) are not right answers.
Since \( \quad \cos \beta \gt 0 \), \( \sec \beta \gt 0 \), hence D) is not the right answer.
\( \sin \beta + \cos \beta = 1 \) is valid for \( k = 0 \) only and therefore E) is not the right answer.
The identity \( \cos^2 \beta + \sin^2 \beta = 1 \) gives \( \cos \beta = \pm \sqrt{1-sin^2\beta} \)
In this situation \( \cos \beta \gt 0 \) and therefore
\( \cos \beta = \sqrt{1-sin^2\beta} \) is valid for any value of \( k \) hence C) is the right answer.
- Answer: A
Solution
Expand \(\quad \cos (\theta + 3\pi) = \cos \theta \cos 3\pi - \sin \theta \sin 3\pi \)
Simplify and substitute: \( \quad \cos (\theta + 3\pi) = - \cos \theta = - 1/5 \)
- Answer: C
Solution
We start with the range of the basic sine function: \( \quad -1 \le \sin(2x-\pi/4)\le 1 \)
Multiply all terms of the above inequality by \( \quad - \dfrac{1}{3} \) and reverse the inequality signs : \( \dfrac{1}{3} \ge - \dfrac{1}{3} \sin(2x-\pi/4)\ge - \dfrac{1}{3} \)
Subtract \( 3 \) from all terms of the inequality: \( \quad \dfrac{1}{3} - 3 \ge - \dfrac{1}{3} \sin(2x-\pi/4) - 3\ge - \dfrac{1}{3} - 3\)
Note that the term in the middle of the inequality is \( f(x) \); simplfy and rewrite the inequality with the smallest terms on the left: \( \quad -\dfrac{10}{3} \le f(x) \le - \dfrac{8}{3} \)
The range of the given function is given by the interval: \( \left[ -\dfrac{10}{3} , - \dfrac{8}{3} \right] \)
- Answer: E
Solution
The zeros of \( f(x) \) are the solutions to the trigonometric equation: \( \quad 2 \cos (2x - \pi/3) + 1 = 0 \)
Let \( y = 2x - \pi/3 \) and rewrite the equation in terms of \( y \) as follows: \( \cos y = - 1/2\)
The reference angle \( y_r \) that is a solution to the equation: \( \cos y = 1/2\) is given by: \( y_r = \dfrac{\pi}{3} \)
The solutions to the equation \( \quad \cos y = - 1/2\) are given by: \( \quad y_1 = \pi - y_r + 2 n \pi \) and \( y_2 = \pi + y_r + 2 n \pi \) , where \( n \) is any integer.
Substitute to obtain: \( \quad y_1 = \dfrac{2\pi}{3} + 2 n \pi \) and \( \quad y_2 = \dfrac{4\pi}{3} + 2 n \pi \)
Use the substitution \( y = 2x - \pi/3 \) to write the equations in \( x \): \( 2x_1 - \pi/3 = \dfrac{2\pi}{3} + 2 n \pi \) and \( 2x_2 - \pi/3 = \dfrac{4\pi}{3} + 2 n \pi \)
Solve for \( x \): \(\quad x_1 = \dfrac{\pi}{2} + n \pi \) and \( x_2 = \dfrac{5\pi}{6} + n \pi \)
There is an infinite number of solutions but we need the solutions in the interval \( [0,\pi) \). Set \( n = 0 \) to obtain the solutions: \( \quad x_1 = \dfrac{\pi}{2} \) and \( x_2 = \dfrac{5\pi}{6} \)
Note that any other values of the integer \( n \) would give solutions outside the interval \( [0,\pi) \)
- Answer: D
Solution
The range of the given function \( \quad f(x) = - \sin (x + \pi/6) + 1 \) is \( [0,2] \) and therefore the maximum of \( f(x) \) value is equal to \( 2 \)
The values of \( x \) for which the given function \( \quad f(x) = - \sin (x + \pi/6) + 1 \) is equal to the maximum value \( 2 \) are found by solving the equation: \( - \sin (x + \pi/6) + 1 = 2\)
Rewrite the equation as: \(\sin (x + \pi/6) = - 1\)
The solutions to the above equation are given by \( \quad x + \pi/6 = \dfrac{3\pi}{2} + 2 n \pi \) , where \( n \) is any integer.
Solve for \( x \): \( \quad x = \dfrac{4\pi}{3} + 2 n \pi \)
The is an infinite number of zeros but only one zero in the intrerval \( [0,2\pi) \) given by: \( x = \dfrac{4\pi}{3} \)
- Answer: A
Solution
The period of a function of the form \( \quad f(x) = A \cos (Bx + C ) + D \) is given by: \( \dfrac{2 \pi}{|B|} \)
Hence the period of \( \quad f(x) = - \cos (-\dfrac{x}{4} - 2 \pi) + 10 \) is equal to \( \dfrac{2 \pi}{\left|\dfrac{-1}{4}\right|} = 8\pi \)
- Answer: B
Solution
The amplitude of a function of the form \( \quad f(x) = A \cos (Bx + C ) + D \) is given by: \( |A| \)
Hence the period of \( \quad f(x) = - 2 \cos (-5x - \pi) + 5 \) is equal to \( |-2| = 2 \)
- Answer: D
Solution
We need to find \( A \) , \( B \), \( C \) and \( D \) in the function \( f(x) = A \sin(B x + C) +D \) with given conditions.
\( B \gt 0\), period = \( \pi/2 = \dfrac{2\pi}{B} \). Solve for \( B \) to find \( B = 4 \).
\( A \gt 0 \) positive, amplitude = \( 2 = A \)
Hence \( f(x) = 2 \sin(4 x + C) + D \)
To have a maximum value of the function equal to \( 3 \), \( D \) must be equal to \( 1 \).
A maximum at \( x = \pi/4 \) gives the equation: \( \quad 2 \sin(4 (\pi/4) + C) + 1 = 3 \)
Rearrange the above equation: \( \sin(4 (\pi/4) + C) = 1 \)
The above equation gives: \( 4 (\pi/4) + C = \pi/2 + 2 n \pi \)
Solve for \( C \) to obtain: \( C = - \pi/2 + 2 n \pi \)
Several solutions for \( C \); for \( n = 0 \), we obtain \( C = - \pi/2 \)
Hence: \( f(x) = 2 \sin(4 x - \pi/2 ) + 1 \)
- Answer: C
Solution
From the graph, the amplitude is equal to \( 2.5 \) , hence \( A = 2.5 \)
From the graph the period is equal to: \( 2\pi/3 \), hence \( 2\pi/3 = 2\pi / B \), solve for \( B = 3 \)
\( f(x) \) has a minimum value equal at \( - 2.5 \) at \( x = \dfrac{0+\pi/3}{2} = \pi/6 \)
Hence \( f(\pi/6) = 2.5 cos( 3(\pi/6) +C) = -2.5 \)
Rewrite the above equation as: \( cos( \pi/2 +C) = - 1 \)
Solve: \( \pi/2 +C = \pi \) which gives \( C = \pi/2 \)
Hence: \( f(x) = 2.5 \cos(3 x + \pi/2) \)
- Answer: E
Solution
Given \( \quad \dfrac{\cos x - \sin x}{1 - \tan x} \)
Multiply numerator and denominator of the given expression by \( \cos x + \sin x \) to obtain \( \quad \dfrac{(\cos x - \sin x)(\cos x + \sin x)}{(1 - \tan x)(\cos x + \sin x)} \)
Substitute \( \tan x \) by \( \dfrac{\sin x}{\cos x} \) : \( \quad \dfrac{(\cos x - \sin x)(\cos x + \sin x)}{(1 - \dfrac{\sin x }{\cos x})(\cos x + \sin x)} \)
Rewrite as: \( \quad \dfrac{(\cos x - \sin x)(\cos x + \sin x)}{(\cos x - \sin x )(\cos x / \cos x + \sin x / \cos x)} \)
Divide numerator and denominator by \( \cos x - \sin x \) and simplify to obtain: \( \quad \dfrac{\cos x - \sin x}{1 - \tan x} = \dfrac{\cos x + \sin x}{1 + \tan x} \)
- Answer: C
Solution
We first expand \( \quad \cos (\alpha - \beta) = \cos \alpha \cos \beta + \sin \alpha \sin \beta \). We therefore need to find \( \cos \alpha \), \( \cos \beta \) and \( \sin \beta \).
Given \( \quad \sin \alpha = 9/15 = \dfrac{opposite \; side}{hypotenuse} \) and \( \quad \tan \beta = 28/45 = \dfrac{opposite \; side}{adjacent \; side}\), we represent angles \( \alpha \) and \( \beta \) in right triangles as shown in the figure below (not-to-scale).

We use the Pythagorean theorem to find the side \( a \) adjacent to angle \( \alpha \): \( a = \sqrt{15^2-9^2} = 12 \)
We use the Pythagorean theorem to find the hypotenuse \( h \) making angle \( \beta \) with the adjacent side: \( h = \sqrt{28^2+45^2} = 53 \)
Angle \( \alpha \) is in quadrant II and therefore \( \cos \alpha \lt 0 \); angle \( \beta \) is in quadrant III and therefore \( \cos \beta \lt 0 \) and \( \sin \beta \lt 0 \)
We now use the right triangles, taking into account the signs in the different quadrants, to calculate: \( \cos \alpha = - \dfrac{12}{15}\), \( \cos \beta = - \dfrac{45}{53} \), \( \sin \beta = - \dfrac{32}{53} \)
We now substitute: \( \quad \cos (\alpha - \beta) = (- \dfrac{12}{15})( - \dfrac{45}{53}) + (\dfrac{9}{15}) (- \dfrac{32}{53}) = \dfrac{84}{265} \)
- Answer: A
Solution
Use the law of sines : \( \dfrac{\sin A}{a} = \dfrac{\sin B}{b} \)
Substitute by known values and solve for \( \sin B \): \( \sin B = \dfrac{b}{a} \sin A = \dfrac{12}{22} \sin 42^{\circ} = 0.36498 \)
Calculate angle \( B \): \( B = \arcsin (0.36498) \approx 21.41^{\circ \:}\)
Hence angle \( C \) is given by: \( C \approx 180^{\circ \:} - 42^{\circ \:} - 21.41^{\circ \:} \approx 116.59^{\circ \:} \)
- Answer: B
Solution
Use the law of cosines : \( a^2 = b^2 + c^2 - 2 b c \cos A \)
Substitute by known values and solve for \( \cos A \): \( \cos A = \dfrac{24^2 - 30^2 - 32^2}{- 2 (30) (32) } = \dfrac{337}{480} \)
Calculate angle \( A \): \( A = \arccos (\dfrac{337}{480}) \approx 45.41^{\circ \:}\)
- Answer: E
Solution
Given the trigonometric equation
: \( \quad 2 \sin (3 x - \pi/2) + 2 = 1\)
Rewrite with sine on one side \( \quad \sin (3 x - \pi/2) = -1/2 \)
Let \( \theta = 3 x - \pi/2 \) and write the above equation as: \( \quad \sin (\theta) = -1/2 \)
Solve the above equation for \( \theta \) which gives two sets of solutions: \( \quad \theta_1 = \dfrac{7\pi }{6}+2\pi n \) and \( \theta_2 = \dfrac{11\pi }{6}+2\pi n \)
Substitute \( \theta \) by \( 3 x - \pi/2 \): \( \quad 3 x_1 - \pi/2 = \dfrac{7\pi }{6}+2\pi n \) and \( 3 x_2 - \pi/2 = \dfrac{11\pi }{6}+2\pi n \)
Solve the two equations for \( x \): \( \quad x_1 = \dfrac{5\pi}{9} + \dfrac{2 n \pi}{3}\) and \( \quad x_2 = \dfrac{7\pi}{9} + \dfrac{2 n \pi}{3}\)
- Answer: D
Solution
Given the trigonometric equation
: \( \quad \tan x + \cot x = - 2\)
Rewrite the given equation using the trigonometric identity \( \cot x = 1 / \tan x \): \( \quad \tan x + 1 / \tan x = - 2\)
Let \( u = \tan x \) and rewrite the equation in terms of \( u \): \( \quad u^2 + 2 u + 1 = 0\)
Solve for \( u \): \( u = - 1\)
Solve for \( x \): \( u = \tan x = - 1 \)
General solutions: \( x = \dfrac{3 \pi}{4} + n \pi \) and two solutions: \( x_1 = \dfrac{3 \pi}{4} \) and \( x_1 = \dfrac{7 \pi}{4} \) on the inteval \( [0, 2\pi)\)
- Answer: B
Solution
Given the trigonometric equation
: \( \quad 2 \sin^2 x + 3\cos^2 x = 5/2 \)
Multiply all terms by \( 2 \), simplify and rewrite as: \( \quad 4 \sin^2 x + 6\cos^2 x = 5 \)
Use the identity: \( \quad \cos^2 x = 1- \sin^2 x \) and rewrite the equation as: \( \quad 4 \sin^2 x + 6(1- \sin^2 x) = 5 \)
Simplify and rewrite the equation as: \( \quad 2 \sin^2 x = 1 \)
Solve for \( \sin x \): \( \sin x_1 = \dfrac{1}{\sqrt 2} \) and \( \sin x_2 = - \dfrac{1}{\sqrt 2} \)
General solutions: \( x_1 = \dfrac{\pi}{4} + 2 n \pi \) and \( x_2 = \dfrac{3 \pi}{4} + 2 n \pi\)
Solutions on the interval \( [0,2\pi) \): \( \quad x_1 = \dfrac{\pi}{4} \) and \( x_2 = \dfrac{3 \pi}{4} \)
- Answer: D
Solution
Relationship between polar coordinates \( \quad (r , \theta) \) and rectangular coordinates \( (x , y) \) are given by: \( x = r \cos \theta \) and \( y = r \cos \theta \)
Which gives: \( \quad \tan \theta = \dfrac{y}{x} = -5/2 \) and \( r^2 = x^2 + y^2 \)
Reference angle \( \theta_r \) to \( \theta \) is found by solving the equation: \( \quad \tan \theta_r = 5/2 \) which gives \( \theta_r = \arctan (5/2) \)
The given point \( (-2,5) \) is in quadrant II, hence \( \quad \theta = \pi - \theta_r = \pi - \arctan (5/2) \)
\( \quad r = \sqrt {(-2)^2 + 5^2} = \sqrt {29}\)
The polar coordinates of the given point are: \( \quad (\sqrt {29} \; , \; \pi - \arctan (5/2)) \)
- Answer: B
Solution
The circumference of the circular path is given by: \( C = 2 \pi \times 2.1 \)
The number of rotations per minute is given by: \( \dfrac{250.4}{2 \pi \times 2.1} = 18.97733 \) rotations per minute.
Each rotation correspond to \( 2\pi \) and each minute corresponds to \( 60 \) seconds.
The angular speed is given by: \( \dfrac{18.97733 \times 2\pi}{60} = 1.99 \) radians/second
- Answer: A
Solution
Arc length: \( \quad S = r \theta = 1.2 \) , hence \( r = \dfrac{1.2}{\dfrac{32^{\circ} \times \pi}{180}} = 2.14859 \) meters
Area of Sector: \( \quad A = 0.5 r^2 \theta = 0.5 \times 2.14859^2 \times {\dfrac{32^{\circ} \times \pi}{180}} = 1.29 \) square meters.
- Answer: C
Solution
Expand the given expression: \( \quad \quad \sin\left(\arccos\left(-0.5\right)+\dfrac{\pi }{4}\right) = \sin \; \arccos(-0.5) \;\; \cos \dfrac{\pi }{4} + \cos \; \arccos(-0.5) \;\; \sin \dfrac{\pi }{4} \)
\( \arccos(-0.5) = 2\pi/3 \)
Simplify: \( \quad \sin (2\pi/3) \dfrac{\sqrt 2}{2} - 0.5 \dfrac{\sqrt 2}{2} = \dfrac{\sqrt 3}{2} \dfrac{\sqrt 2}{2} - 0.5 \dfrac{\sqrt 2}{2} = \dfrac{\sqrt 6 - \sqrt 2}{4} \)
More References and Links
Trigonometry Questions and Problems
More placement tests practice
Free Algebra Questions and Problems with Answers




