College Algebra Placement Test Practice with Solutions
The following multiple choice college algebra questions guide you in assessing your skills and abilities in the following topics: functions, their domains and range, properties of graphs of functions,
transformations of functions, composite and inverse functions, quadratic functions, rational functions, equation of a line, equation of a circle, solving higher order polynomial equations, exponential and
logarithmic functions and equations, piecewise functions, matrices and systems of equations are presented along with their answers and detailed solutions.
You are not allowed to solve any of these questions using a calculator. You may use a calculator for basic calculations only.
Questions for Algebra Placement Practice
-
The domain of the function \( f(x) = \dfrac{\sqrt {x-1}}{\sqrt{2-x}} \) is given by the interval
- \( ( -\infty , \infty ) \)
- \( ( -\infty , 2 ) \)
- \( [ 1 , 2 ) \)
- \( [ 1 , 2 ] \)
- \( [ 1 , \infty ) \)
-
The range of function \( f \) whose graph is shown below

, is given by
- \( \displaystyle [ - 3 , 3 ] \)
- \( \displaystyle ( - 3 , 3 ) \)
- \( \displaystyle [ - 3 , - 1) \cup (0 , 2 ] \cup \{3\} \)
- \( \displaystyle [ - 3 , - 1) \cup (0 , 2 ] \)
- \( \displaystyle [ - 3 , - 1] \cup [ 0 , 2 ] \cup \{3\} \)
-
Function \( f \) is given by a table and function \( g \) is given by a graph. Which of the followoing is closest to the value of \( \dfrac{f(g(1))}{(g_o f)(6)} \)?

- 3
- \(\dfrac{1}{3}\)
- \(\dfrac{1}{4}\)
- 1
- 4
-
If \( f(\dfrac{x-1}{x+3}) = 3x - 2 \), then \( f(x) = \)
- \( 3x - 2 \)
- \( \dfrac{x-1}{x+3} \)
- \( \dfrac{11x-1}{x-1} \)
- \( \dfrac{-11x-1}{x+3} \)
- \( \dfrac{-11x-1}{x-1} \)
-
If the graph of \( f(x) \) is obtained by shifting and reflecting the graph of \( y = \sqrt x \), then \( f(x) = \)
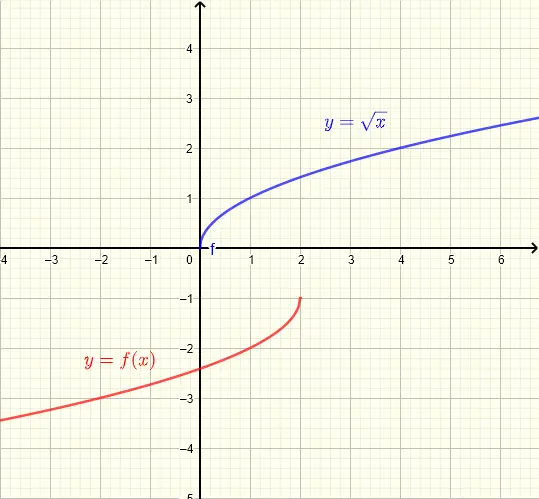
- \( \sqrt{-x} - 1 - \sqrt{2} \)
- \( - \sqrt{-2x + 2} - 1 \)
- \( - \sqrt{2x + 2} - 1 \)
- \( - \sqrt{2 - x} - 1 \)
- \( - \sqrt{x + 2} - 1 \)
-
If \( f(x) = -x^2 - 2x + 3 \) , for x \( \le - 1 \), then \( f^{-1}(x) = \)
- \( - 1 - \sqrt {4-x} \)
- \( - 1 + \sqrt {4-x} \)
- \( - \sqrt {4-x} \)
- \( \sqrt {4-x} \)
- \( \dfrac{1}{ -x^2 - 2x + 3 } \)
-
If \( log_a(x) = A \) and \( log_a(1/y) = B \), then \( log_a(x y^3) = \)
- \( A B \)
- \( A + 3 B \)
- \( \dfrac{A}{3B} \)
- \( A - 3 B \)
- \( \dfrac{A}{B^3} \)
-
The solution set of the equation \( 9^x - 4^x = 6^x \) is given by
- \( \left\{\dfrac{\ln \left(\dfrac{2+\sqrt{5}}{2}\right)}{ \ln \left(\dfrac{3}{2}\right)} \right\} \)
- \( \left\{\dfrac{\ln \left(\dfrac{1+\sqrt{5}}{2}\right)}{ \ln \left(\dfrac{3}{2}\right)} \right\} \)
- \( \left\{\dfrac{\ln \left(\dfrac{-1+\sqrt{5}}{2}\right)}{ \ln \left(\dfrac{3}{2}\right)} \right\} \)
- \( \left\{\dfrac{-\ln \left(\dfrac{1+\sqrt{5}}{2}\right)}{ \ln \left(\dfrac{3}{2}\right)} \right\} \)
- \( \left\{\dfrac{\ln \left(\dfrac{1+\sqrt{5}}{2}\right)}{ \ln \left(\dfrac{5}{2}\right)} \right\} \)
-
The solution set of the equation \( 2\; \ln \left(x-1\right)- \ln\left(x+2\right) = 0 \) is given by
- \( \left\{ \dfrac{3+\sqrt{13}}{2} , \dfrac{3-\sqrt{13}}{2} \right\} \)
- \( \left\{ 3 \right\} \)
- \( \left\{ \dfrac{3 - \sqrt{13}}{2} \right\} \)
- \( \left\{ 1 \right\} \)
- \( \left\{ \dfrac{3+\sqrt{13}}{2} \right\} \)
-
If \( i^2 = - 1 \) and \( a, b \) and \( c \) are real numbers, what is the imaginary part of the complex number \( \dfrac{a}{b + c i} \)?
- \( \dfrac{a}{c} \)
- \( \dfrac{ac}{b^2 - c^2} \)
- \( - \dfrac{a}{c} \)
- \( \dfrac{-ac}{b^2 - c^2} \)
- \( \dfrac{1}{c} \)
-
If \( f(x) = \dfrac{k!(x-2)!}{(k-1)!} \), where \( k \) is a constant, and \( f(2) = 4 \), what is the value of \( k \)?
- \(0\)
- \(1\)
- \(4\)
- \(5\)
- \(6\)
-
The sum of the first \( 20 \) terms of a geometric sequence is \( -1398100 \) and its common ratio is equal to \( -2 \). What is the value of the \( 5^{th} \) term in the sequence?
- \( 64 \)
- \( 32 \)
- \( 128 \)
- \( 16 \)
- \( 5 \)
-
In an arithmetic sequence, the first term of the sequence is -3, the sum of the first \( 10 \) terms is \( -15/2 \). What are the first 3 terms?
- \( a_1 = -3 , a_2 = -3\dfrac{1}{2}, a_3 = - 4 \)
- \( a_1 = -3 , a_2 = -2\dfrac{1}{2}, a_3 = - 2 \)
- \( a_1 = -3 , a_2 = -2 , a_3 = - 1 \)
- \( a_1 = -3 , a_2 = -4\dfrac{1}{2}, a_3 = - 6 \)
- \( a_1 = -3 , a_2 = -1 , a_3 = 1 \)
-
Find \( k \) such that the determinant of the matrix \(\begin{bmatrix}
1 & 0 & -3\\
-1 & k & -2\\
-2 & -3 & 3
\end{bmatrix} \) is equal to 0.
- \( 2 \)
- \( - 3 \)
- \( 5 \)
- \( - 5 \)
- \( 4 \)
-
Find all values of \( m \) for which the quadratic equation \( -x^2 + m x = m + 8 \) has two distinct real solution.
- \( (-\infty , -4) \cup (8 , \infty) \)
- \( (-\infty , \infty) \)
- \( (-\infty , -4) \)
- \( (8 , \infty) \)
- \( (-4 , 8) \)
-
Find the solution set of the equation \( - \sqrt{-x+2} + 3 = - 5\).
- \( x = - 2 \)
- \( x = - 14 \)
- \( x = - 34 \)
- \( x = - 62 \)
- \( x = - 79 \)
-
Find the solution set of the equation \( \left(\dfrac{x}{x-1}\right)^2 + \dfrac{x}{x-1} = 2 \).
- \( x = 2 \)
- \( x = \dfrac{2}{3} \)
- \( x = \dfrac{3}{2} \)
- \( x = -1 \)
- \( x = -2 \)
-
Find the solution set of the inequality \( |2x - 1| \ge 2 \).
- \( \left[\dfrac{3}{2} , \infty \right) \)
- \( \left(-\infty , -\dfrac{1}{2} \right) \)
- \( \left(-\infty , - \dfrac{1}{2} \right) \cup \left(\dfrac{3}{2} , \infty \right) \)
- \( \left( \dfrac{3}{2} , \infty \right) \)
- \( \left(-\infty , - \dfrac{1}{2} \right] \cup \left[\dfrac{3}{2} , \infty \right) \)
-
Find the area of the circle whose equation
is given by \( x^2 - 2x + y^2 + 3y = 5 \).
- \( 25 \pi \)
- \( 5 \pi \)
- \( 33 \pi \)
- \( \dfrac{33 \pi}{4} \)
- \( 4 \pi \)
-
Find the equation of the line through the point \( (2,3) \) and perpendicular
to the line with equation\( \quad -2y + x = 5 \).
- \( \quad y = - \dfrac{1}{2} x + 7 \)
- \( \quad y = - 2 x + 7 \)
- \( \quad y = 2 x + 7 \)
- \( \quad y = - 2 x \)
- \( \quad y = 2 x - 7 \)
-
What is the horizontal asymptote of the graph of the function \( f(x) = \dfrac{ (-2x-1)^2}{3x^2 - 9} \).
- \( y = - \dfrac{2}{3} \)
- \( y = \dfrac{2}{3} \)
- \( y = \dfrac{4}{3} \)
- \( y = - \dfrac{4}{3} \)
- \( y = - \dfrac{1}{9} \)
-
For what value of \( k \) does the system of equation \( 2 x - 3y = 3 , - x - 2 k y = 5 \) have no solution?
- \( k = -\dfrac{3}{4} \)
- \( k = 0 \)
- \( k = -\dfrac{5}{2} \)
- \( k = \dfrac{3}{4} \)
- \( k = -\dfrac{4}{3} \)
-
\( x - 2 \) is a factor of the polynomial \( P(x) = x^3-8x^2+21x-18 \). Find the solution set of the equation \( x^3-8x^2+21x-18 = 4(x - 2) \).
- {1,2,0}
- {1,2,8}
- {-1,2,-5}
- {1,-2,5}
- {1,2,5}
-
If \( f(x) =
\begin{cases}
-4 & x\le -2 \\\\
\dfrac{x}{x-1} & -2 \lt x \leq 4 \\\\
-x^2 +1/2 & 4 \gt x
\end{cases} \),
then the value of \( f(-2) + f(4) = \)
- \( \dfrac{2}{5} \)
- \( -\dfrac{8}{3} \)
- \( \dfrac{5}{2} \)
- \( \dfrac{8}{3} \)
- \( -\dfrac{2}{5} \)
Answers and Solutions to the Above Questions
- Answer: D
Solution
For \( f(x) \) to have real values we need to have: \( x-1 \ge 0 \) and \( 2 - x \gt 0 \)
The solution set to the inequality \( x-1 \ge 0 \) is given by the interval: \( [1 , \infty) \)
The solution set to the inequality \( 2 - x \gt 0 \) is given by the interval: \( (-\infty , 2) \)
The domain of function \( f \) is given by the intersection of the two intervals found above and is given by \( [1 , 2) \)
- Answer: C
Solution
For \( x \) in the interval \( [-3,-1) \), the range of the values of the function is within the interval \( [-3,-1) \)
For \( x \) in the interval \( [-1,1) \), the range of the values of the function is within the interval \( (0,2] \)
For \( x \ge 1 \), the range of the values of the function is \( \{3 \} \)
The range of the function is the union of all all three intervals found above: \( [-3,-1) \cup (0,2] \cup \{3 \} \)
- Answer: A
Solution
\( f(g(1)) = f(0) = 3 \)
\( (g_o f)(6) = g(f(6)) = g(4) = 1 \)
\( \dfrac{f(g(1))}{(g_o f)(6)} = 3/1 = 3 \)
- Answer: E
Solution
Let \( u = \dfrac{x-1}{x+3} \)
Solve the above for \( x \) to obtain: \( x = \dfrac{-3u-1}{u-1} \)
Substitute \( \dfrac{x-1}{x+3} \) by \( u \) and \( x \) by \( \dfrac{-3u-1}{u-1} \) in \( f(\dfrac{x-1}{x+3}) = 3x - 2 \) to obtain
\( f(u) = 3 \dfrac{-3u-1}{u-1} - 2 \)
Simplify the above to obtain
\( f(u) = \dfrac{-11 u-1}{u-1} \) or \( f(x) = \dfrac{-11x - 1}{x - 1} \)
- Answer: D
Solution
To obtain the graph of \( f \) from that of \( \sqrt x \), we first need to reflect the graph of \( \sqrt x \) on the x axis to obtain \( - \sqrt x \)
We next shift \( - \sqrt x \) on the y axis to obtain \( - \sqrt {-x} \)
We then shift \( - \sqrt {-x} \) 2 units to the right to obtain \( - \sqrt {-(x-2)} = - \sqrt {-x+2} \)
then 1 unit down to obtain \( f(x) = - \sqrt {2 - x} - 1\)
- Answer: A
Solution
Let \( y = -x^2 - 2x + 3 \) and complete the square on the right side
\( y = - (x + 1)^2 + 4 \)
Solve the above for \( x \) to obtain two solutions: \( x = - 1 \pm \sqrt {4-y} \)
Since \( x \le -1 \), we select the solution \( x = - 1 - \sqrt {4-y} \)
Hence \( f^{-1} (x) = - 1 - \sqrt {4-x} \)
- Answer: D
Solution
Use the product and power rules of logarithmic functions to write: \( \quad log_a(x y^3) = log_a \; x + 3 log_a \; y \)
Use quotient rule to write: \( \quad log_a(1/y) = log_a \; 1 - log_a \; y = B \) , hence \( log_a \; y = - B \)
Substitute to obtain \( \quad log_a(x y^3) = log_a \; x + 3 log_a \; y = A - 3 B\)
- Answer: B
Solution
Given: \( 9^x - 4^x = 6^x \)
Divide all terms of the equations by the term \( 4^x \) to obtain the equation: \( \quad \dfrac{9^x}{4^x} - \dfrac{4^x}{4^x} = \dfrac{6^x}{4^x} \)
Use exponents rules to simplify and rewrite as: \( \quad (\dfrac{9}{4})^x - 1 = (\dfrac{6}{4})^x \)
The above equation may be rewritten as: \( \quad ((\dfrac{3}{2})^2)^x - 1 = (\dfrac{3}{2})^x \)
Let \( u = (\dfrac{3}{2})^x \) and substitute in the above equation to rewrite it as: \( \quad u^2 - 1 = u \)
Solve the above quadratic equation to obtain the solutions: \( \quad u = \dfrac{1\pm\sqrt{5}}{2} \)
But \( \quad u = (\dfrac{3}{2})^x \) is positive, hence the solution is \( \quad u = \dfrac{1+\sqrt{5}}{2} = (\dfrac{3}{2})^x \)
Solve for \( x \) the above equation; take the \( \ln \) of both sides: \( \quad \ln \left(\dfrac{1+\sqrt{5}}{2}\right) = \ln \left((\dfrac{3}{2})^x \right) \)
Simplify to obtain the solution \( \quad x = \dfrac{\ln \left(\dfrac{1+\sqrt{5}}{2}\right)}{ \ln \left(\dfrac{3}{2}\right)} \)
- Answer: E
Solution
Given: \( \quad 2\; \ln \left(x-1\right)- \ln\left(x+2\right) = 0 \)
Use power and quotient rules of logarithms to group the left hand side of the equation and the fact that \( \ln 1 = 0\) to rewrite the given equation as: \( \ln \dfrac{\left(x-1\right)^2}{\left(x+2\right)} = \ln 1 \)
The logarithmic function is a one to one function and therefore the above equation gives the algebraic equation: \( \dfrac{\left(x-1\right)^2}{\left(x+2\right)} = 1 \)
Solve the above to obtain the solutions: \( x=\dfrac{3+\sqrt{13}}{2} , \: x=\dfrac{3-\sqrt{13}}{2} \)
We now need to substitute the solutions obtained above and check if they are solutions to the given equation.
Use a calculator and check that the solution to the original equation is: \( x = \dfrac{3+\sqrt{13}}{2} \)
- Answer: D
Solution
Given: \( \dfrac{a}{b + c \; i} \)
Multiply numerator and denominator by the complex conjugate of the denominator \( \dfrac{a(b - c \; i)}{(b + c \; i)(b - c \; i)} \)
Multiply and simplify: \( \dfrac{a b - a c \; i}{b^2 - c^2} \)
Write in standard form: \( \dfrac{a b}{b^2 - c^2} + \dfrac{-ac}{b^2 - c^2} \; i \)
The imaginary part of the given complex number is: \( \dfrac{-ac}{b^2 - c^2} \)
- Answer:C
Solution
Given: \( f(x) = \dfrac{k!(x-2)!}{(k-1)!} \), and \( f(2) = 4 \)
\( f(2) = \dfrac{k!(2-2)!}{(k-1)!} \)
Note that \( 0! = 1 \) and \( k! = k (k - 1)! \)
Hence \( f(2) = \dfrac{k(k-1)!1}{(k-1)!} = k = 4 \)
- Answer:A
Solution
The sum \( S_n \) of the first \( n \) terms of geometric sequence is given by \( S_n = \dfrac{a_1(1-r^n)}{1-r} \) , common ration \( r = - 2 \)
Hence \( \dfrac{a_1(1-(-2)^{20})}{1-(-2)} = -1398100\) gives \( a_1 = 4 \)
The \( n^{th} \) of a geometric sequence is given by \( a_n = a_1 r^{n-1} \)
Hence the fifth term \( a_5 = 4 (-2)^{5-1} = 64\)
- Answer: B
Solution
The sum \( S_n \) of the first \( n \) terms of an arithmetic sequence is given by: \( S_n = \dfrac{n}{2}(2 a_1 + (n-1) d ) \) where \( a_1 \) is the first term and \( d \) is the common difference.
Hence \( S_{10} = \dfrac{10}{2}(2 (-3) + (10 - 1) d ) = -15/2 \)
Solve for \( d \) to obtain \( d = 1/2 \)
The first three terms \( a_1, a_2 \) and \( a_3 \) are given by: \( a_1 = -3 \) , \( a_2 = -3 +1/2 = -2\dfrac{1}{2} \) , \( a_3 = - 3 + 1/2 + 1/2 = - 2 \)
- Answer: D
Solution
The determinant of the matrix
\(\begin{bmatrix}
1 & 0 & -3\\
-1 & k & -2\\
-2 & -3 & 3
\end{bmatrix} \) is given by \( 1 \times (3 k - 6) - 0 + (-3) \times (3 + 2 k) = -3 k - 15 \)
For the determinant to be zero, we need to solve the equation \( -3 k - 15 = 0 \) and obtain \( k = - 5 \)
- Answer: A
Solution
Given the quadratic equation \( -x^2 + m x = m + 8 \)
Which may be written in standard form as \( -x^2 + m x - m - 8 = 0 \)
Calculate the discriminant of the above quadratic equation in \( m \): \( \quad \Delta = m^2 - 4 (-1)(-m - 8) = m^2 - 4 m - 32 \)
The given equation has two distinct solutions if \( \quad \Delta \gt 0 \) or \( m^2 - 4 m - 32 \gt 0 \)
The left side of the inequality may be factored as \( \quad (m - 8)(m + 4) \gt 0 \)
The solution set of the above inequality is given by: \( \quad (-\infty , -4) \cup (8 , \infty) \)
Hence the set of all values of \( m \) for which the equation has two distinct solution is given by the interval: \( (-\infty , -4) \cup (8 , \infty) \)
- Answer: D
Solution
Given the equation \( - \sqrt{-x+2} + 3 = - 5\)
Rewrite the equation with the radical on one side: \( \sqrt{-x+2} = 8\)
Square both sides: \( (\sqrt{-x+2}) ^2 = 8^2\)
Simplify: \( -x + 2 = 64\)
Solve for x: \( x = -62 \)
Substitute \( x \) by \( -62 \) to check Solution in the original equation, : \( \quad - \sqrt{-(-62)+2} + 3 = - 5\)
Simplify: \( - 8 + 3 = - 5\) ,
Hence \( x = -62 \) is the solution to the given equation.
- Answer: B
Solution
Given the equation: \( \quad \left(\dfrac{x}{x-1}\right)^2 + \dfrac{x}{x-1} = 2 \)
Let \( u = \left(\dfrac{x}{x-1}\right) \)
Substitute and rewrite the given equation in terms of \( u \): \( \quad u^2 + u = 2 \)
Solve the above quadratic equation to obatin two solutions: \( u = -2 \) and \( u = 1\)
Substitute and solve for \( x \) the equations: \( u = \left(\dfrac{x}{x-1}\right) = - 2 \) and \( u = \left(\dfrac{x}{x-1}\right) = 1 \)
One solution only: \( x = 2/3 \)
- Answer: E
Solution
Given the inequality \( \quad |2x - 1| \ge 2 \)
The above inequality may be rewritten as \( \quad 2x - 1 \ge 2 \) or \( 2x - 1 \le - 2 \)
Solve the above: \( \quad x \ge 3/2 \) or \( x \le - 1 / 2\)
The above solution set in interval form may be written as follows: \( \quad (-\infty , -1/2 ] \cup [3/2 , \infty) \)
- Answer: D
Solution
Given \( \quad x^2 - 2x + y^2 + 3y = 5 \)
Complete the square in \( x \) and \( y \) on the left side: \( \quad (x-1)^2 -1 + (y + 3/2)^2 - 9/4 = 5 \)
Rewrite in standard form: \( \quad (x-1)^2 + (y + 3/2)^2 = 33/4 \)
Hence the radius of the circle is equal to: \( \quad \sqrt {33}/2 \)
The area of the circle is equal to: \( \quad \pi ( \sqrt {33}/2 )^2 = \dfrac{33\pi}{4} \)
- Answer: B
Solution
Given: A point \( (2,3) \), perpendicular to the line with equation \( \quad -2y + x = 5 \)
The line \( \quad -2y + x = 5 \) in
slope intercept form : \( \quad y = \dfrac{1}{2} x - \dfrac{5}{2} \)
The slope \( m \) of the is equal to \( \dfrac{1}{2} \)
The slope \( m' \) of the line perpendicular with slope \( m = \dfrac{1}{2} \) are related by: \( m m' = - 1 \)
Hence \( m' = - 2 \)
The equation of the line through \( (2,3) \) and perpendicular to the line with equation \( \quad -2y + x = 5 \) is given by: \( \quad y - 3 = m' (x - 2) \) which may be written in slope intercept form as: \( \quad y = - 2 x + 7 \)
- Answer: C
Solution
Given the function: \( \quad f(x) = \dfrac{ (-2x-1)^2}{3x^2 - 9} \)
Expand the numerator of the given function: \( \quad f(x) = \dfrac{ 4x^2 + 4x + 1}{3x^2 - 9} \)
The given function is a rational function with the degrees of the numerator and denominator equal; hence the horizontal asymptote is given by: \( \quad y = 4/3 \)
- Answer: A
Solution
Given the system: \( \quad 2 x - 3y = 3 , - x - 2 k y = 5 \)
We first define the determinants used in Cramer's rules :
\( D = Det \begin{bmatrix}
2 & -3 \\
-1 & - 2k
\end{bmatrix} = -4k-3
\)
\( D_x = Det \begin{bmatrix}
3 & -3 \\
5 & - 2k
\end{bmatrix} = -6k + 15
\)
\( D_y = Det \begin{bmatrix}
2 & 3 \\
-1 & 5
\end{bmatrix} = 13
\)
Since \( D_y \) is not equal to zero, the given system of equations has no solutions if \( D = 0 \)
, hence
\( -4k-3 = 0 \) which gives the solution \( k = -3/4 \)
- Answer: E
Solution
Since \( x - 2 \) is a factor of the polynomial \( P(x) = x^3-8x^2+21x-18 \), then \( P(x) = (x-2)Q(x) \)
Using division of polynomials, we can find \( P(x) = \dfrac{P(x)}{x-2} = \dfrac{x^3-8x^2+21x-18}{x-2} = \left(x-3\right)^2 \)
We now write \( P(x) = \left(x-3\right)^2 (x-2) \)
Substitute \( P(x) \) in the equation to solve
\( \left(x-3\right)^2 (x-2) = 4(x-2) \)
Write the above equation with zero on the right side
\( \left(x-3\right)^2 (x-2) - 4(x-2) = 0 \)
Factor the left side
\( (x-2)(\left(x-3\right)^2 - 4) = 0 \)
Solve \( x - 2 = 0 \) to obtain the solution \( x = 2 \)
Solve \( \left(x-3\right)^2 - 4 = 0 \) to obtain the solutions \( x = 1 \) and \( x = 5 \)
Hence the solution set of the given equation is \( \{ 1,2,5 \} \)
- Answer: B
Solution
\( -2 \) is within the interval defined by \( x \le -2 \) hence \( f(-2) = -4 \)
\( 4 \) is within the interval defined by \( -2 \lt x \le 4 \) hence \( f(4) = \dfrac{4}{4-1} = \dfrac{4}{3}\)
\( f(-2) + f(4) = -4 + 4/3 = -8/3 \)
More References and Links
College Algebra Questions With Answers
More placement tests practice
Free Algebra Questions and Problems with Answers


