The following multiple choice geometry questions guide you in assessing your skills and abilities in the following topics: triangles and their properties, quadrilateral and their properties, angles formed by parallel and secant lines, tangent to circles, inscribed and central angles, rectangles and circles, rigth triangles and the Pythagorean theorem, trapezoids, spheres and cylinders are presented along with their answers and detailedsolutions.
Questions for Geometry Placement Tests Practice
Note that none of the figures included in the questions and answers are drawn to scale.
Which of the following is not correct?
I) A line tangent to a circle intersects the circle one point only called point of tangency. A line through the center of the circle and the point of tangency is perpendicular to the tangent line.
II) The longer side in a triangle is greater the sum of the other two sides.
III) A triangle with two equal angles is an isosceles triangle.
IV) The opposite sides of a parallelogram are parallel but not congruent (equal in size).
V) Two triangles with congruent (equal in size) angles are similar and their corresponding sides are proportional.
VI) The size of an angle inscribed in a semicircle is greater than \( 90^{\circ} \).
VII) The sum of all interior angles of a quadrilateral is equal to \( 360^{\circ} \)
A) (II) only
B) (IV) and (V)
C) (V)
D) (II) and (III)
E) (II) , (IV) and (VI).
Find \( x \) in the figure below.
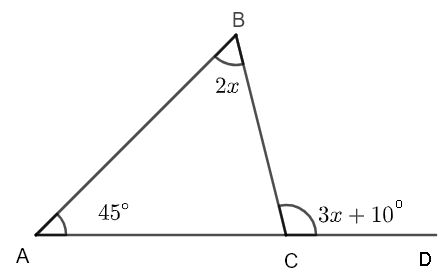
A) \( 35^{\circ} \)
B) \( 25^{\circ} \)
C) \( 26^{\circ} \)
D) \( 27^{\circ} \)
E) \( 34^{\circ} \)
Calculate the area of the isosceles triangle in the figure below.
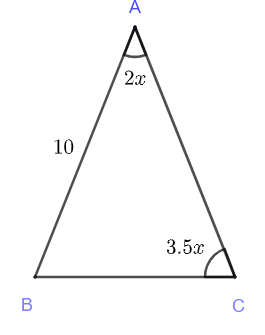
A) \( 100 \sin (65.45^{\circ })\) square units
B) \( 50 \sin (65.45^{\circ })\) square units
C) \( 50 \sin (40^{\circ })\) square units
D) \( 50 \) square units
E) \( 100 \sin (40^{\circ })\) square units
Calculate the area of the quadrilateral in the figure below and approximate the answer to 2 decimal places.
A) \( 44.06 \) square units
B) \( 22.03 \) square units
C) \( 88.12 \) square units
D) \( 105.00 \) square units
E) \( 52.50 \) square units
Find the area of the rectangle \( AEFG \) given that the sum of the areas of the triangles \( ABC \) and \( CDE \) is equal to \( 200 \) square units..
A) \( 800 \) square units
B) \( 400 \) square units
C) \( 200 \) square units
D) \( 600 \) square units
E) \( 500 \) square units
In the figure below \( AB \) is parallel to \( CD \). What is the size of \( \angle CHF \) ?
A) \( \quad 112^{\circ} \)
B) \( \quad 56^{\circ} \)
C) \( \quad 22^{\circ} \)
D) \( \quad 68^{\circ} \)
E) \( \quad 90^{\circ} \)
What is the size of \( \angle GAF \) in the figure below?
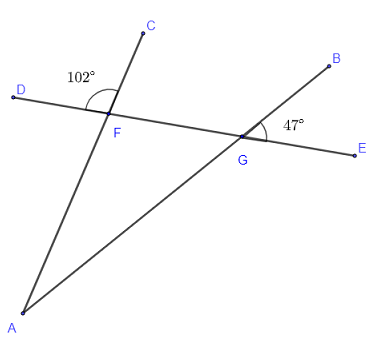
A) \( \quad 47^{\circ} \)
B) \( \quad 31^{\circ} \)
C) \( \quad 55^{\circ} \)
D) \( \quad 35^{\circ} \)
E) \( \quad 45^{\circ} \)
\( ABCD \) is a rectangle of width \( 80 \) and length \( 240 \), and the circle shown in the figure is tangent to \( AE , EF, FD \) and \( DA \) with \( EF \) parallel to \( AE \). Find the area of the shaded (orange) surface in the diagram below.
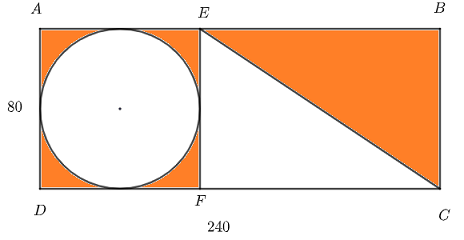
A) \( \quad 12800 \) square units
B) \( \quad 19200 + 1600 \pi \) square units
C) \( \quad 19200 - 1600 \pi \) square units
D) \( \quad 12800 + 1600 \pi \) square units
E) \( \quad 12800 - 1600 \pi \) square units
Which of the following is a right triangle ? (Note the sides of the triangle are labeled by \( a, b \text{ and } c \) and the opposite angles by \( A, B \text{ and } C\) ).
(I): \( a = 0.3 \;, \; b = 0.4 \; , \; c = 0.5 \) (II): \( A = 23^{\circ} \;, \; B = 80^{\circ} \) (III): \( C = 34^{\circ} \;, \; B = 56^{\circ} \) (IV): \( a = 2 \;,\; b = 4 \;,\; c = 5 \)
A) (I), (II), (III) and (IV)
B) (II) and (III) only
C) (I) and (III) only
D) (I) and (II) only
E) (III) only
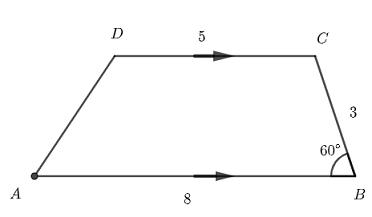
Find the area of the trapezoid \( ABCD \) shown below.
A) \( \quad \dfrac{39\sqrt{3}}{4} \) square units
B) \( \quad \dfrac{39}{4} \) square units
C) \( \quad 24 \) square units
D) \( \quad 15 \) square units
E) \( \quad \dfrac{39\sqrt{3}}{2} \) square units
Calculate the area of \( \triangle ODB \) and round it to \( 2 \) decimal places.
A) \( 252.87\) square units
B) \( 272.72 \) square units
C) \( 440.25 \) square units
D) \( 660.12 \) square units
E) \( 230.66 \) square units
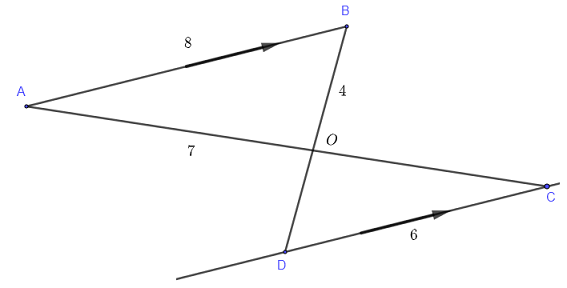
In the diagram below, \( AB \) is parallel to \( DC \). Find the length of segment \( OC \).
A) \( 3 \)
B) \( 12 \)
C) \( \dfrac{24}{7} \)
D) \( \dfrac{21}{4} \)
E) \( \dfrac{4}{21} \)
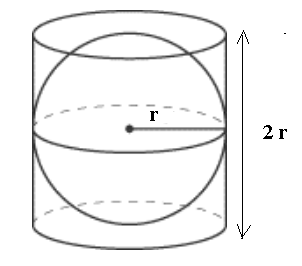
A sphere of radius \( r \) is inscribed in a cylinder with a height equal to \( 2 r \). Find the volume of the cylinder if the volume of the sphere is \( 3000 \) cubic units.
A) \( 2000 \) cubic units
B) \( 4500 \) cubic units
C) \( 5000 \) cubic units
D) \( 3500 \) cubic units
E) \( 4000 \) cubic units \)
In the diagram below, \( AD \) and \( AC \) are tangent to the circle. Find the size of angle \( CBD \).
A) \( 124^{\circ} \)
B) \( 56^{\circ} \)
C) \( 62^{\circ} \)
D) \( 34^{\circ} \)
E) \( 68^{\circ} \)
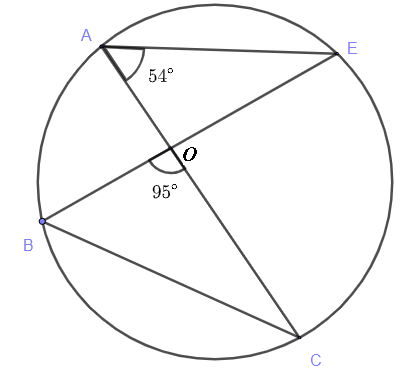
Find the size of \( \angle ACB \) in the diagram below.
A) \( 30^{\circ} \)
B) \( 60^{\circ} \)
C) \( 41^{\circ} \)
D) \( 49^{\circ} \)
E) \( 31^{\circ} \)
Which of the following is not correct?
I) A square is a rhombus.
II) A rectangle is a parallelogram.
III) A square is not a parallelogram.
IV) A trapezoid is not a quadrilateral.
V) A kite has equal adjacent sides.
VI) A parallelogram has its opposite sides parallel but not necessarily equal.
VII) A rhombus is not a parallelogram.
A) (III) only
B) (IV) only
C) (III) and (VII) only
D) (III), (IV), (VI) and (VII)
E) (VI) and (VII) only.
Answers and Solutions to the Above Questions
Answer E
Solution
The statement in (II) , (IV) and (VI) are not correct. The corresponding correct statement are:
(II) : The sum of any two sides of a triangle is greater than the third side.
(IV) : The opposite sides of a parallelogram are both parallel and congruent.
(VI) : The size of angle inscribed in a semicircle is equal to \( 90^{\circ} \).
Answer A
Solution
Angles \( ACB \) and \( BCD \) make a straight angle and therefore their sum is equal to \( 180^{\circ} \)
Hence: \( \quad \angle ACB + 3x + 10 = 180 \)
Solve for \( \angle ACB \) to obtain: \( \quad \angle ACB = 170 - 3x \)
The sum of all interior angles in a triangle is equal to \( 180^{\circ} \), hence: \( \quad 45 + 2x + (170 - 3x) = 180 \)
Solve the above equation for \( x \): \( \quad x = 35^{\circ} \)
Answer C
Solution
We first need to find \( x \) and then the angles. The triangle is isosceles and therefore angles \( ABC \) and \( ACB \) have equal sizes.
The sum of all interior angle in the given triangle is equal to \( 180^{\circ} \), hence the equation : \( \quad 3.5 x + 3.5 x + 2x = 180 \)
Solve for \( x \) to obtain: \( \quad x = 20 \)
The size of angle \( BAC \) is given by \( 2x = 40^{\circ} \)
The area \( A \) of the triangle using sine formula is given by: \( \quad A = (1/2)\times 10 \times 10 \times \sin 40^{\circ} = 50 \sin (40^{\circ })\) square units
Answer A
Solution
One way to calculate the area \( A \) of a quadrilateral such as the one given above is to calculate the areas \( A_1 \) and \( A_2 \) of triangles \( ACD \) and \( ABC \) respectively and add them.
The area \( A_1 \) of triangle \( ACD \) is given by: \( \quad A_1 = (1/2) \times 9 \times 7 \times \sin 94^{\circ} \)
In order to find the area of triangle \( ABC \), we first need to find the size of angle \( ABC \) using the cosine rule as follows:
Use the cosine rule in triangles triangles \( ACD \) and \( ABC \) to write \( \quad AC^2 = a^2 + b^2 - 2 \times a \times b \times \cos 94^{\circ} = c^2 + d^2 - 2 \times c \times d \times \cos \angle ABC \)
Substitute the known quantities to obtain the equation: \( \quad 9^2 + 7^2 - 2 \times 9 \times 7 \times \cos 94^{\circ} = 6^2 + 7^2 - 2 \times 6 \cdot 7 \times \cos \angle ABC \)
Solve for \( \cos \angle ABC \): \( \quad \cos \angle ABC = \dfrac{126\cos (94^{\circ \:})-45}{84} \)
Hence: \( \quad \angle ABC = \arccos (\dfrac{126\cos (94^{\circ \:})-45}{84}) = 129.82^{\circ} \)
The area \( A_2 \) of triangle \( ABC \) is given by: \( \quad A_2 = (1/2) \times 6 \times 7 \times \sin 129.82^{\circ} \)
The area of the quadrilateral is given by: \( \quad A = A_1 + A_2 = 44.06 \) square units.
Answer B
Solution
Note that the height \( AG \) of the rectangle \( AEFG \) and all the heights of the triangles inside the rectangle are equal to \( h = AG \)
Area \( A_1 \) of triangle \( ABC \) is given by: \( (1/2) \times AC \times h \)
Area \( A_2 \) of triangle \( CDE \) is given by: \( (1/2) \times CE \times h \)
The area \( A_r \) of the rectangle \( AEFG \) is given by: \( A_r = AE \times h \)
\( A_1 + A_2 = (1/2) AC \times h + (1/2) CE \times h = (1/2) \times (AC+CE) \times h = (1/2) \times AE \times h \)
When comparing \( A_r \) and \( A_1 + A_2 \), we can see that \( A_r = 2(A_1 + A_2) = 2 \times 200 = 400 \) square units
Answer D
Solution
The corresponding angles \( \quad \angle AGE \) and \( \angle CHG \) are equal; hence \( \angle CHG = 112^{\circ} \)
Angles \( \angle CHG \) and \( \angle CHF \) are supplementary and therefore \( \quad \angle CHG + \angle CHF = 180^{\circ} \)
Hence: \( \quad \angle CHF = 180^{\circ} - 112^{\circ} = 68^{\circ} \)
Answer B
Solution
Angles \( \angle CFD \) and \( \angle GFA \) are vertical and therefore their sizes are equal. Hence \( \angle GFA = 102^{\circ} \)
Angles \( \angle BGE \) and \( \angle AGF \) are vertical and therefore their sizes are equal. Hence \( \angle FGA = 47^{\circ} \)
The sum of all interior angles in the triangle \( FAG \) is equal to \( 180^{\circ} \); hence: \( \angle GAF + 102^{\circ} + 47^{\circ} = 180^{\circ} \)
Solve for \( \angle GAF \) to obtain: \( \angle GAF = 180^{\circ} - 149^{\circ} = 31^{\circ} \)
Answer E
Solution
The area \( A_r \) of the shaded surface is obtained by subtracting the areas of the non shaded surfaces which are the circle and the right triangle \( EFC \) from the area of the rectangle \( ABCD \).
Area of the rectangle \( ABCD \) is given by: \( \quad A_1 = 80 \times 240 = 19200 \) square units
Area \( A_2 \) of the circle is given by: \( \quad A_2 = \pi \times 40^2 = 1600 \pi \) square units.
The area \( A_3 \) of the right triangle \( EFC \) is given by: \( \quad A_3 = \dfrac{1}{2} 80 \times (240 - 80) = 6400 \) square units.
The total area \( A_r \) of the shaded surface is given by: \( \quad A_r = A_1 - A_2 - A_3 = 19200 - 1600 \pi - 6400 = 12800 - 1600 \pi \) square units
Answer C
Solution
(I) : We are given the 3 sides in (I) and we therefore need to use the Pythagorean theorem in order to determine whether the given triangle is a right triangle.
The square of the largest side is: \( \quad c^2 = 0.5^2 = 0.25\)
The sum of the squares of the two smallest sides: \( \quad a^2 + b^2 = 0.3^2 + 0.4^2 = 0.25 \)
Hence: \( \quad c^2 = a^2 + b^2 \) and therefore the given triangle is a right triangle.
(II) : The third angle in (II) is given by: \( \quad 180^{\circ} - 23^{\circ} - 80^{\circ} = 77^{\circ}\)
The given triangle is not a right triangle.
(III) : The third angle in (III) is given by: \( \quad 180^{\circ} - 34^{\circ} - 56^{\circ} = 90^{\circ}\)
The given triangle is a right triangle.
(IV) : We are given the 3 sides in (IV) and we therefore need to use the Pythagorean theorem.
The square of the largest side is: \( \quad c^2 = 5^2 = 25\)
The sum of the squares of the two smallest sides: \( \quad a^2 + b^2 = 2^2 + 4^2 = 20 \)
Hence: \( \quad c^2 \ne a^2 + b^2 \) and therefore the given triangle is not a right triangle.
Answer A
Solution
We first need to find the height \( h \) of the trapezoid as shown in the diagram below: \( \quad h = 3 \sin 60^{\circ} \)
The area \( A \) of the trapezoid is given by: \( \quad A = \dfrac{1}{2} (AB+DC)\; h = \dfrac{1}{2} (5 + 8) 3 \sin 60^{\circ} = \dfrac{39\sqrt{3}}{4} \) square units
Answer A
Solution
Angles \( DOB \) and \( AOC \) are vertical and therefore have equal sizes.
Using the sine formula , the area \( A \) of triangle \( ODB \) is given by: \( \quad A = \dfrac{1}{2} \times OD \times OB \sin 68^{\circ} \)
We now use the intersecting chords theorem to write: \( \quad OD \times OC = OA \times OB \)
Substitute the known quantities and solve for \( OD \): \( \quad 22 \; OD = 600 \) , hence \( OD = \dfrac{300}{11} \)
The area \( A \) is given by: \( \quad A = \dfrac{1}{2} \times \dfrac{300}{11} \times 20 \sin 68^{\circ} = \quad \dfrac{3000\sin \left(68^{\circ }\right)}{11} \approx 252.87\) square units
Answer D
Solution
Use the intercept theorem to write: \( \quad \dfrac{AB}{DC} = \dfrac{OA}{OC} \)
Substitute the known quantities: \( \quad \dfrac{8}{6} = \dfrac{7}{OC} \)
Solve for \( OC \): \( \quad OC = \dfrac{21}{4} \)
Answer B
Solution
Volume \( V_c \) of the cylinder is given by: \( \quad \quad V_c = \pi r^2 (2r) = 2 \pi r^3 \)
Volume \( V_s \) of the sphere is given by: \( \quad \quad V_s = \dfrac{4}{3} \pi r^3 \)
The ratio \( \quad \dfrac{V_c}{V_s} = \dfrac{2 \pi r^3}{ \dfrac{4}{3} \pi r^3} = 3/2 \)
Hence: \( \quad V_c = (3/2) V_s = (3/2) 3000 = 4500 \) cubic units
Answer C
Solution
We first draw segments \( OD \) and \( OC \) where \( O \) is the center of the circle and therefore \( OD \) is perpendicular to \( AD \) and \( OC \) is perpendicular to \( AC \).
Note that the inscribed angle \( DBC \) and the central angle \( DOC \) intercept the same arc \( CD \) hence according to the theorem on inscribed and central angles we have:
\( \quad \angle DBC = \dfrac{1}{2} \angle DOC \)
We now write the sum of all angles in the quadrilateral \( ACOD \) is equal to \( 360^{\circ} \)
\( \quad 56 + 90 + 90 + \angle DOC = 360 \)
Solve for \( \angle DOC = 124^{\circ}\)
Hence \( \quad \angle DBC = \dfrac{1}{2} \times 124 = 62^{\circ} \)
Answer E
Solution
Angles \( CAE \) and \( CBE \) intercept the same arc and according to the theorem on inscribed angles they are have equal sizes. Hence
\( \quad \angle CBE = \angle CAE = 54^{\circ} \)
We now write the sum of all angles in the triangle \( CBO \) is equal to \( 180^{\circ} \)
\( \quad \angle CBE + 95 + \angle ACB = 180 \)
Hence \( \quad \angle ACB = 180 - 95 - 54 = 31^{\circ} \)
Answer D
Solution
The statement in (III), (IV), (VI) and (VII) are not correct. The corresponding correct statement are:
(III) : A square is a parallelogram because its opposite sides are parallel.
(IV) : A trapezoid is a quadrilateral since it has 4 sides.
(VI) : A parallelogram has its opposite sides parallel and are equal.
(VII): A rhombus is a parallelogram since its opposite sides are parallel and equal.
